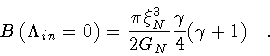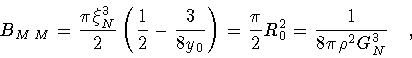Next: 7. Conclusion Up: Classical and Quantum Shell Previous:
5. Quantum Mechanics
Let us consider, for example, the classical motion of
a shell in the potential of Fig.2.
Figure:
Graphical representation, in a generic case, of the effective
potential described by equation (48).
Typically, there are
three distinct
trajectories. Two of them are classically allowed: (A)
bounded, and (C) unbounded. Trajectory (B)
is classically forbidden and corresponds to quantum
mechanical tunneling through the potential barrier. The
exponential of the action evaluated along B
gives the WKB approximation to the tunneling amplitude from A
to C.
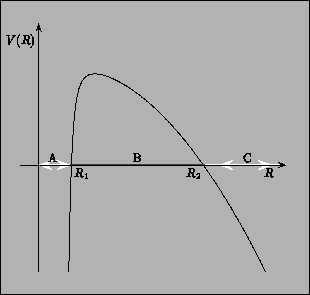 |
The classically allowed trajectories for the shell
are: A (bounded), i.e., the shell starts at R=0,
expands reaching a maximum radius at R1 and then
re-collapses to R=0, or C (unbounded), i.e., the
shell starts with unbounded radius, contracts reaching
a minimum radius at R2 and then re-expands to infinity.
The quantum mechanical amplitude for the shell to tunnel
from one classically allowed trajectory (A) to the
other (C), is proportional to the exponential of
the integral of the Euclidean momentum PE calculated
along the Euclidean trajectory B which interpolates
between the two classical ones, namely
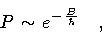 |
(66) |
where
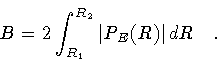 |
(67) |
The Euclidean momentum PE is given by
eq.(52).
Along the Euclidean trajectory, using the equation of motion
H=0, that equation can be rewritten as
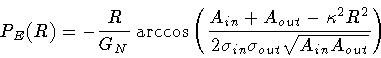 |
(68) |
with
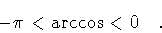 |
(69) |
Inserting PE(R) in eq.(67), integrating
by parts, taking into account the vanishing of PE at
the turning points R1 and R2, one finally obtains
| B |
= |
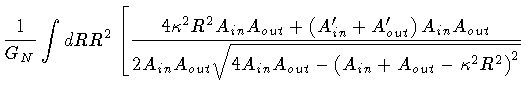 |
|
| |
|
![$\displaystyle \qquad -
\left.
\frac{ A^2_{in} A'_{out} +
A'_{in} A^2_{out} -
\k...
..._{out}
-
\left(
A_{in} + A_{out} - \kappa ^2 R^2
\right) ^2
}
}
\right]
\quad .$](img175.gif) |
(70) |
where the symbol `` ' '' means differentiation with respect to R.
In order to check the consistency of our formulation, in the
remainder of this section we shall revisit the problem of vacuum
decay and the influence of gravity on it. This subject was discussed in a
seminal paper by Coleman and De Luccia [16], and also by
Parke [17], using simple semi-classical and geometrical arguments.
Our intent, then, is to show how their results follow
from the dynamical framework discussed so far.
The system under consideration consists of two de Sitter domains joined
along the spherical shell 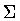 ,
which is characterized
by a constant surface tension
,
which is characterized
by a constant surface tension 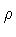 .
In other words, we assign
.
In other words, we assign
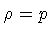 as equation of state; then, equation (17)
implies
as equation of state; then, equation (17)
implies
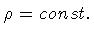 ,
which is assumed to be positive.
Therefore, the form of the metric in the interior and exterior regions is
,
which is assumed to be positive.
Therefore, the form of the metric in the interior and exterior regions is
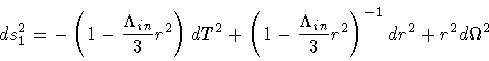 |
(71) |
and
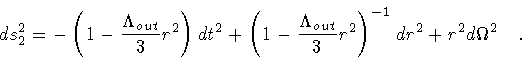 |
(72) |
The Hamiltonian of the shell is obtained from eq.(37)
![\begin{displaymath}H = - \frac{R}{G_N} \left[
\sigma _{in}
\sqrt{1 -
\frac{\L...
... _{out}}{3} R^2 +
\dot{R}^2
}
-
\kappa R
\right]
\quad .
\end{displaymath}](img180.gif) |
(73) |
In order to simplify the notation, let us introduce two parameters
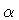 and
and 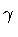 such that
such that
and rescale the shell radius and proper time by a factor
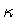
Then the coefficients of the metric become
| Ain |
= |
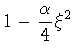 |
(78) |
| A out |
= |
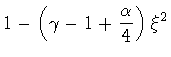 |
(79) |
and the equation of motion, after dividing by R, can be
rewritten
as
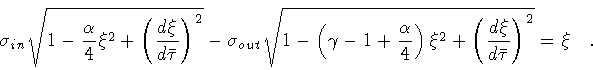 |
(80) |
After squaring eq.(80) we arrive at
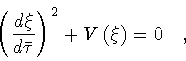 |
(81) |
where
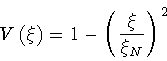 |
(82) |
and
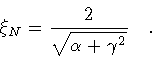 |
(83) |
Equation(81) is integrated with the initial
condition
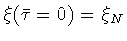 ,
so that
,
so that
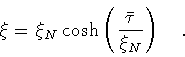 |
(84) |
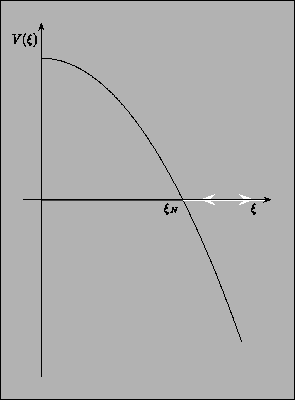
The potential 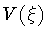 is represented in
fig.3.
is represented in
fig.3.
Figure:
Graphical representation of the effective potential 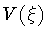 for the
situation in which the ``in'' and ``out'' geometries are of
de Sitter type.
for the
situation in which the ``in'' and ``out'' geometries are of
de Sitter type. 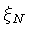 will be referred to as the ``nucleation radius''.
The diagram displays only the unbounded trajectory,
since the bounded one is degenerate (
will be referred to as the ``nucleation radius''.
The diagram displays only the unbounded trajectory,
since the bounded one is degenerate (
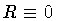 ).
Note that only for
).
Note that only for
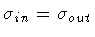 this is a
classical solution of eq.(48).
this is a
classical solution of eq.(48).
 |
The classical motion corresponds to a shell (separating
the two de Sitter spaces) which starts at
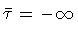 with an infinite radius, contracts to a minimum radius
with an infinite radius, contracts to a minimum radius
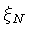 at
at
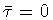 ,
and then expands again
to infinity. From the equation of motion, taking into
account eqs.(45-46), we determine the sign
of the
,
and then expands again
to infinity. From the equation of motion, taking into
account eqs.(45-46), we determine the sign
of the 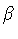 's as follows
's as follows
For the purpose of illustrating our method, consider the case
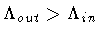 ,
thus fixing
,
thus fixing
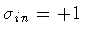 .
Then,
from eq.(86) and (75), we have
.
Then,
from eq.(86) and (75), we have
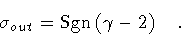 |
(87) |
Thus, we have to consider two possibilities :
- 1.
-
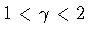 ,
i.e.
,
i.e.
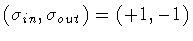
- 2.
-
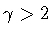 ,
i.e.
,
i.e.
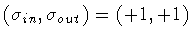
which correspond to the spacetime conformal diagrams shown in
fig.4 and fig.5, respectively.
Figure:
Penrose diagrams corresponding to the ``in'' (a), and the
``out'' (b) domains in
the case
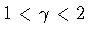 . The light regions correspond
to the physical domains. The side of the diagram in which the
trajectories are drawn is determined by the sign of
. The light regions correspond
to the physical domains. The side of the diagram in which the
trajectories are drawn is determined by the sign of
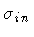 and
and
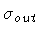 . Their sign is also
related to the
direction of the normal to the shell orbit.
. Their sign is also
related to the
direction of the normal to the shell orbit.
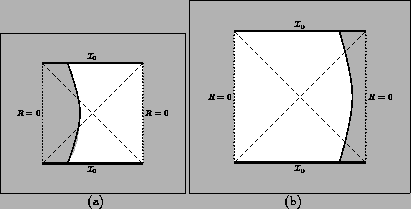 |
Figure:
Penrose diagrams corresponding to the ``in'' (a), and the
``out'' (b) domains in the case
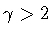 . Comparing with
Fig.(4), note that the
change of sign of
. Comparing with
Fig.(4), note that the
change of sign of
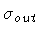 is reflected by the fact that the
shell trajectory is now drawn in the opposite half of the conformal diagram.
is reflected by the fact that the
shell trajectory is now drawn in the opposite half of the conformal diagram.
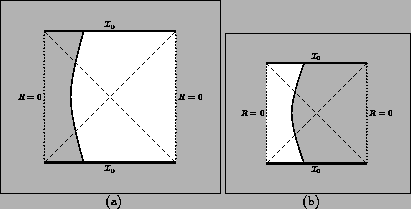 |
The physical spacetime is obtained by ``gluing" along
 the un-dashed regions of each figure.
the un-dashed regions of each figure.
Let us consider first case # 2,
 .
From the Hamiltonian of
eq.(73), we see that
the configuration R=0 (i.e., no shell,
the whole spacetime is de Sitter ``out'')
satisfies the constraint H=0. On the other hand,
our previous analysis of the classical motion revealed
that classically allowed configurations for the
shell exist only for shell radii
.
From the Hamiltonian of
eq.(73), we see that
the configuration R=0 (i.e., no shell,
the whole spacetime is de Sitter ``out'')
satisfies the constraint H=0. On the other hand,
our previous analysis of the classical motion revealed
that classically allowed configurations for the
shell exist only for shell radii
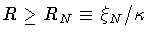 ,
where RN
represents the turning point.
,
where RN
represents the turning point.
Let us recall that false vacuum decay is a
quantum process which proceeds via the nucleation of true vacuum bubbles
of a given non-vanishing radius which then expand
filling the surrounding false vacuum region. In our approach,
this process (the formation of one bubble) is described
by the quantum mechanical tunneling through the barrier
represented in fig.3, from the R=0 shell
configuration to one for which R=RN. In terms of conformal
diagrams, the process is visualized in fig.6.
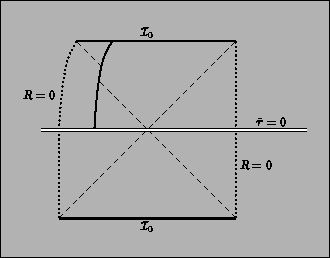
Figure:
Penrose diagram corresponding to tunneling along the
classically forbidden trajectory of Fig.(3),
in the case
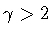 . Tunneling occurs at
. Tunneling occurs at
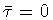 and nucleates
a true vacuum bubble in the false vacuum background.
and nucleates
a true vacuum bubble in the false vacuum background.
 |
The probability of this process is given, in the WKB
approximation, and apart from an overall factor, by
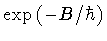 ,
where B
is given by eq.(70). In order to calculate the nucleation
coefficient B for the present case, it is useful to define
,
where B
is given by eq.(70). In order to calculate the nucleation
coefficient B for the present case, it is useful to define
| y0 -1 |
= |
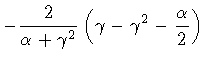 |
(88) |
| y1 -1 |
= |
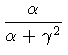 |
(89) |
| y2 -1 |
= |
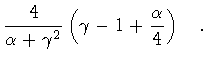 |
(90) |
Note that, since
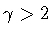 ,
all three constants are
positive.
The nucleation coefficient B then becomes
,
all three constants are
positive.
The nucleation coefficient B then becomes
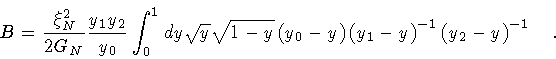 |
(91) |
Performing the integration in the complex plane, as described
in
Appendix C, we
obtain
Then, with some lengthy algebra, which we confine to Appendix
D, one can show that the nucleation
radius and the nucleation coefficient B coincide exactly with the
expression obtained by Parke [17].
A simpler case worth considering here, is the limiting value of B,
given by eq.(92), as
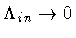 .
In this case
.
In this case
![\begin{displaymath}B \left( \Lambda _{in} = 0 \right )
=
\frac{\pi \xi _N^3}{2...
..._2}{y_2 - 1}
\right) ^{\frac{1}{2}}
\right)
\right]
\quad ,
\end{displaymath}](img224.gif) |
(94) |
which, after unfolding the expression of the constants, takes the form
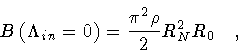 |
(95) |
where RN represents the nucleation radius of the bubble,
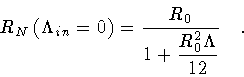 |
(96) |
Equations(95-96) reproduce exactly the results obtained by
Coleman and de Luccia[16].
As a final remark, and in preparation of the next case, note that in
the previous discussion the initial configuration R=0 consists of the
classical spacetime obtained by letting
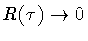 in
fig.5.b, with
in
fig.5.b, with
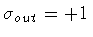 during the whole process. Therefore, in that limit
the shaded region of fig.5.b disappears,
leaving as initial configuration for the tunneling process the
whole de Sitter spacetime.
during the whole process. Therefore, in that limit
the shaded region of fig.5.b disappears,
leaving as initial configuration for the tunneling process the
whole de Sitter spacetime.
Consider now case # 1, i.e.,
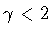 .
In
the same limit as before, but keeping now
.
In
the same limit as before, but keeping now
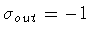 ,
we see from fig.4.b
that all the un-dashed region (which represents the physical region)
disappears. Therefore, in this case we have a peculiar
situation in which the initial configuration corresponds to
no spacetime at all, so that
the tunneling process describes now something rather
different from vacuum decay, which we interpret as the creation
from nothing of a closed universe formed by two de Sitter cups.
,
we see from fig.4.b
that all the un-dashed region (which represents the physical region)
disappears. Therefore, in this case we have a peculiar
situation in which the initial configuration corresponds to
no spacetime at all, so that
the tunneling process describes now something rather
different from vacuum decay, which we interpret as the creation
from nothing of a closed universe formed by two de Sitter cups.
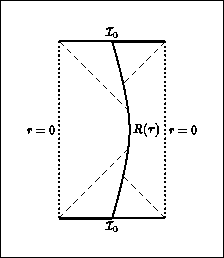
Figure:
Penrose diagram corresponding to tunneling along the
classically forbidden trajectory of Fig.(3),
in the case
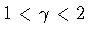 . In this case the configuration
. In this case the configuration
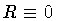 does not represent a classical solution, and one cannot speak
of ``bubble nucleation''. One possible quantum mechanical interpretation
of this process is simply as the birth ``from nothing'' of a
universe composed of two de Sitter domains.
does not represent a classical solution, and one cannot speak
of ``bubble nucleation''. One possible quantum mechanical interpretation
of this process is simply as the birth ``from nothing'' of a
universe composed of two de Sitter domains.
 |
It seems conceivable that this kind of process is characteristic
of the foam structure of spacetime at small scales of length at which
black holes, wormholes and inflationary
domains are continuously created out of the vacuum.
The expression for the nucleation coefficient in this case (
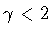 ), is
), is
![\begin{displaymath}B = \frac{\pi \xi _N^3}{2 G_N}
\frac{y_1 y_2}{y_0}
\left[
...
...pha}
\left( 2 \gamma - 2 + \alpha \right)- 1
\right]
\quad .
\end{displaymath}](img231.gif) |
(97) |
For
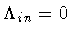 ,
the above expression reduces to
,
the above expression reduces to
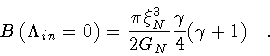 |
(98) |
By considering a further limit,
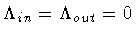 ,
corresponding to
the creation of a Minkowski pair, we obtain
,
corresponding to
the creation of a Minkowski pair, we obtain
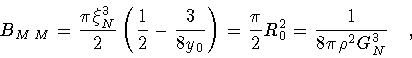 |
(99) |
in exact agreement with the bounce calculation of ref.[18].



Next: 7. Conclusion Up: Classical and Quantum Shell Previous:
5. Quantum Mechanics
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY


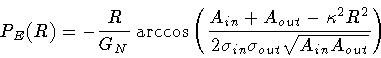
![]() ,
which is characterized
by a constant surface tension
,
which is characterized
by a constant surface tension ![]() .
In other words, we assign
.
In other words, we assign
![]() as equation of state; then, equation (17)
implies
as equation of state; then, equation (17)
implies
![]() ,
which is assumed to be positive.
Therefore, the form of the metric in the interior and exterior regions is
,
which is assumed to be positive.
Therefore, the form of the metric in the interior and exterior regions is
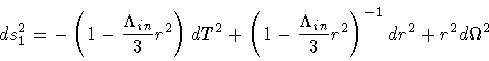
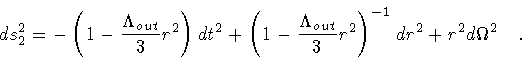
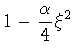
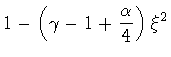
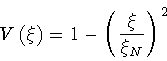
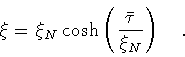



![]() .
From the Hamiltonian of
eq.(73), we see that
the configuration R=0 (i.e., no shell,
the whole spacetime is de Sitter ``out'')
satisfies the constraint H=0. On the other hand,
our previous analysis of the classical motion revealed
that classically allowed configurations for the
shell exist only for shell radii
.
From the Hamiltonian of
eq.(73), we see that
the configuration R=0 (i.e., no shell,
the whole spacetime is de Sitter ``out'')
satisfies the constraint H=0. On the other hand,
our previous analysis of the classical motion revealed
that classically allowed configurations for the
shell exist only for shell radii
![]() ,
where RN
represents the turning point.
,
where RN
represents the turning point.

![]() .
In this case
.
In this case
![\begin{displaymath}B \left( \Lambda _{in} = 0 \right )
=
\frac{\pi \xi _N^3}{2...
..._2}{y_2 - 1}
\right) ^{\frac{1}{2}}
\right)
\right]
\quad ,
\end{displaymath}](img224.gif)
![]() in
fig.5.b, with
in
fig.5.b, with
![]() during the whole process. Therefore, in that limit
the shaded region of fig.5.b disappears,
leaving as initial configuration for the tunneling process the
whole de Sitter spacetime.
during the whole process. Therefore, in that limit
the shaded region of fig.5.b disappears,
leaving as initial configuration for the tunneling process the
whole de Sitter spacetime.
![]() .
In
the same limit as before, but keeping now
.
In
the same limit as before, but keeping now
![]() ,
we see from fig.4.b
that all the un-dashed region (which represents the physical region)
disappears. Therefore, in this case we have a peculiar
situation in which the initial configuration corresponds to
no spacetime at all, so that
the tunneling process describes now something rather
different from vacuum decay, which we interpret as the creation
from nothing of a closed universe formed by two de Sitter cups.
,
we see from fig.4.b
that all the un-dashed region (which represents the physical region)
disappears. Therefore, in this case we have a peculiar
situation in which the initial configuration corresponds to
no spacetime at all, so that
the tunneling process describes now something rather
different from vacuum decay, which we interpret as the creation
from nothing of a closed universe formed by two de Sitter cups.

![\begin{displaymath}B = \frac{\pi \xi _N^3}{2 G_N}
\frac{y_1 y_2}{y_0}
\left[
...
...pha}
\left( 2 \gamma - 2 + \alpha \right)- 1
\right]
\quad .
\end{displaymath}](img231.gif)