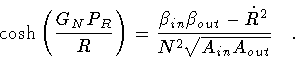Next: 5. Quantum Mechanics Up: Classical and Quantum Shell Previous:
3. Equation of Motion
As discussed in the Introduction, shell-dynamics covers a wide
range of physical situations, from gravitational collapse into black
holes, to wormholes and inflationary bubbles. Several analytical
and graphical methods have been proposed to deal with the
effective dynamics of a shell[13]. From our present
perspective, the essential idea and technical steps can be summarized thus:
let us rewrite the Hamiltonian constraint, taking explicitly into account
the sign multiplicity of the 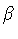 functions,
functions,
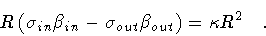 |
(44) |
Squaring this expression, we obtain
![\begin{displaymath}\sigma _{in} = {\rm Sgn} \left[ \kappa
\left(
A _{in} - A _{out}
+
\kappa ^2 R^2
\right)
\right]
\end{displaymath}](img120.gif) |
(45) |
![\begin{displaymath}\sigma _{out} = {\rm Sgn} \left[ \kappa
\left(
A _{in} - A _{out} - \kappa ^2 R^2
\right)
\right]
\quad .
\end{displaymath}](img121.gif) |
(46) |
These relations determine the signs of the 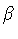 functions
along the shell trajectory.
functions
along the shell trajectory.
Squaring twice the constraint (44), one arrives at a
simple expression for the equation of motion of the shell
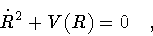 |
(47) |
where
Remarkably, the radial evolution of the shell is governed by an
equation which is equivalent to the classical energy equation of
a unit mass particle moving in a
potential V(R) with zero energy: classically allowed paths require
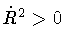 ,
i.e. V(R) < 0. Turning points correspond to
,
i.e. V(R) < 0. Turning points correspond to
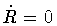 ,
i.e., V(R) = 0. When V(R) > 0
one has
,
i.e., V(R) = 0. When V(R) > 0
one has
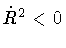 ,
and one speaks of a
forbidden (or Euclidean) trajectory. Thus, using eq.(47),
one can analyze the motion of the shell by specifying, case by case,
the interior and exterior geometry (Ain,
Aout), as well as the shell matter content (
,
and one speaks of a
forbidden (or Euclidean) trajectory. Thus, using eq.(47),
one can analyze the motion of the shell by specifying, case by case,
the interior and exterior geometry (Ain,
Aout), as well as the shell matter content (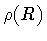 )
[13]. The analysis is facilitated by plotting, on an energy
diagram, the potential curve V(R), together with the horizon
curves (A=0) and the curves corresponding to the vanishing of the
)
[13]. The analysis is facilitated by plotting, on an energy
diagram, the potential curve V(R), together with the horizon
curves (A=0) and the curves corresponding to the vanishing of the
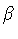 functions. Presently, we simply make some general observations
following from the analysis of eqs.(45-48):
functions. Presently, we simply make some general observations
following from the analysis of eqs.(45-48):
- 1.
- turning points (i.e. zeros of the potential)
exist only if
Ain > 0 and
Aout > 0;
- 2.
- if A>0,
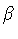 can change sign only
along a forbidden path; if A<0,
can change sign only
along a forbidden path; if A<0, 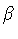 can change sign along a classical path.
can change sign along a classical path.
Furthermore, in the course of the above analysis, one must keep in
mind that the equations of motion were obtained by considering
trajectories which lie in regions where both Killing vectors
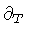 and
and
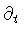 are time-like
(i.e.,
A in > 0 and
A out > 0). When
the above conditions are not satisfied, our
choice of integration volume is no longer appropriate,
since the time variable (t or T) becomes a space-like
coordinate, and does not have a regular behavior at the
horizons (i.e., when A=0). With hindsight, however, since our
effective action correctly leads to Israel's equation
of motion H=0, and makes no reference to the integration volume,
we assume that the expression for S eff is valid for every shell
trajectory when supplemented by a working prescription suggested in
Ref.[7]: when one of the factor A becomes negative, i.e. when
are time-like
(i.e.,
A in > 0 and
A out > 0). When
the above conditions are not satisfied, our
choice of integration volume is no longer appropriate,
since the time variable (t or T) becomes a space-like
coordinate, and does not have a regular behavior at the
horizons (i.e., when A=0). With hindsight, however, since our
effective action correctly leads to Israel's equation
of motion H=0, and makes no reference to the integration volume,
we assume that the expression for S eff is valid for every shell
trajectory when supplemented by a working prescription suggested in
Ref.[7]: when one of the factor A becomes negative, i.e. when
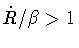 ,
the replacement
,
the replacement
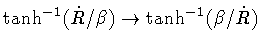 should be understood in
eq.(33).
should be understood in
eq.(33).
The dynamics of the shell can also be analyzed directly in terms of
the Hamiltonian (37)
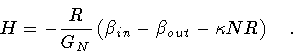 |
(49) |
However, the usefulness of the above expression is limited by the
fact that it is given in implicit form, i.e., it contains
the velocity 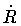 which, in turn, is a function of
the phase space variables (R,PR) obtained by inverting
eq.(36)
which, in turn, is a function of
the phase space variables (R,PR) obtained by inverting
eq.(36)
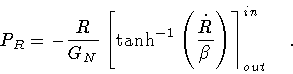 |
(50) |
Therefore, our immediate task is to recast the Hamiltonian in a form
which is more amenable to physical applications, an example of
which will be discussed at the end of this section.
>From equation (50), it follows
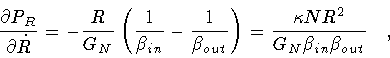 |
(51) |
where the Hamiltonian constraint has been used.
If 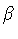 changes sign, then PR is not a monotonic
function of
changes sign, then PR is not a monotonic
function of 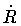 ,
and its inverse is defined only in those
intervals in which eq.(51) is either positive or
negative. As shown before,
,
and its inverse is defined only in those
intervals in which eq.(51) is either positive or
negative. As shown before, 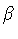 can change sign along a
classical path when A<0 (in this case
can change sign along a
classical path when A<0 (in this case
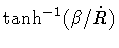 vanishes), or
on a forbidden path, when A>0. In a forbidden region,
vanishes), or
on a forbidden path, when A>0. In a forbidden region,
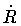 is imaginary, in which case
we define the Euclidean momentum by analytic continuation of
eq.(50)
is imaginary, in which case
we define the Euclidean momentum by analytic continuation of
eq.(50)
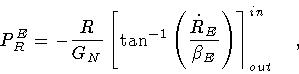 |
(52) |
with
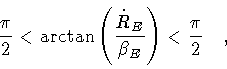 |
(53) |
and
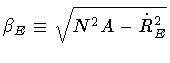 .
Evidently, the above definition is not unique. For instance, the choice of
the interval
.
Evidently, the above definition is not unique. For instance, the choice of
the interval
![$[-\pi , 0]$](img140.gif) (as in ref.[7]),
leads to a non-vanishing PE at turning points when
the
(as in ref.[7]),
leads to a non-vanishing PE at turning points when
the 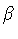 's have opposite sign there. On the other hand, our
choice (53) has the disadvantage that PE is not
continuous when
's have opposite sign there. On the other hand, our
choice (53) has the disadvantage that PE is not
continuous when 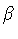 changes sign, i.e.
changes sign, i.e.
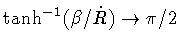 for
for
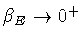 ,
whereas
,
whereas
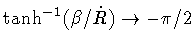 for
for
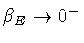 .
In terms of spacetime
diagrams, the vanishing of
.
In terms of spacetime
diagrams, the vanishing of 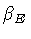 corresponds to an
Euclidean trajectory which jumps from a region
of the Penrose diagram where the normal to the
shell points, say, towards increasing values of
r, to a region where the normal points toward
decreasing values of r. Therefore, we will
limit our considerations only to those systems for which
the
corresponds to an
Euclidean trajectory which jumps from a region
of the Penrose diagram where the normal to the
shell points, say, towards increasing values of
r, to a region where the normal points toward
decreasing values of r. Therefore, we will
limit our considerations only to those systems for which
the 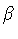 functions have a definite sign. Presumably, some
singular cases such as the quantum mechanical nucleation
of wormholes, which involve
Euclidean trajectories along which
functions have a definite sign. Presumably, some
singular cases such as the quantum mechanical nucleation
of wormholes, which involve
Euclidean trajectories along which 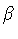 changes
sign, may be dealt with in terms of pseudo-manifolds [7],
or degenerate vierbeins [14].
changes
sign, may be dealt with in terms of pseudo-manifolds [7],
or degenerate vierbeins [14].
Coming back to eq.(50), we can rewrite it as
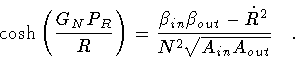 |
(54) |
Then, combining this equation with the implicit form
of the Hamiltonian (49),
one can eliminate the 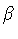 's and
's and 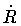 ,
obtaining finally the promised form of the Hamiltonian
,
obtaining finally the promised form of the Hamiltonian
![\begin{displaymath}H = \kappa N R^2
-
\frac{NR}{G_N} \left[
A _{in} +
A _{ou...
...\left( \frac{G_N P}{R} \right)
\right] ^{\frac{1}{2}}
\quad .
\end{displaymath}](img147.gif) |
(55) |
This expression actually corresponds to the case
Ain > 0,
Aout > 0. One can proceed in a similar fashion in
the other cases. A more complete account of the results is
given in Appendix B. Here, however, just to give a sense
of the applicability of this Hamiltonian formulation, we mention a
particular form of the Hamiltonian (55) which
has already appeared in the literature [4]. It
corresponds to a shell of dust (p=0, i.e.,
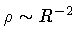 )
separating a Minkowski (interior)
spacetime (
A in = 1,
)
separating a Minkowski (interior)
spacetime (
A in = 1,
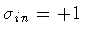 ),
from a Schwarzschild (exterior) one
(
A out = 1 - 2 GN Mout/R,
),
from a Schwarzschild (exterior) one
(
A out = 1 - 2 GN Mout/R,
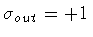 ).
In this case, the matching equation becomes (in the gauge N=1)
).
In this case, the matching equation becomes (in the gauge N=1)
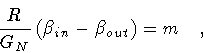 |
(56) |
where m is a constant representing the rest
mass of the shell. In the light of our present formulation, one recognizes the
l.h.s. of eq.(56) as the Hamiltonian of the shell,
![\begin{displaymath}H = \frac{R}{G_N} \left[
2 -
\frac{2 G_N M_{out}}{R} -
2 \...
...eft( \frac{G_N P_R}{R} \right)
\right] ^{\frac{1}{2}}
\quad .
\end{displaymath}](img152.gif) |
(57) |
This expression coincides, up to a constant
term and a sign, with the special form that our eq.(55)
takes under the above hypotheses (
A in = 1,
A out =
1 - 2 GN Mout/R,
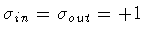 ,
,
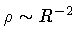 ,
N=1), and leads to the same dynamics. In
Ref.([5]), however, a rather different, and equally arbitrary
construction is performed. In this new interpretation of the model,
(see also ref.[9,11]), after
squaring eq.(56), one identifies
Mout, instead of m, as the numerical
value of the shell proper Hamiltonian which now reads
,
N=1), and leads to the same dynamics. In
Ref.([5]), however, a rather different, and equally arbitrary
construction is performed. In this new interpretation of the model,
(see also ref.[9,11]), after
squaring eq.(56), one identifies
Mout, instead of m, as the numerical
value of the shell proper Hamiltonian which now reads
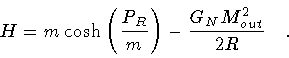 |
(58) |
Note the inequivalence of the two effective
Hamiltonians (57) and (58)
which underscores the arbitrariness of the above constructions in
the absence of a coherent and unified approach to shell dynamics.



Next: 5. Quantum Mechanics
Up: Classical and Quantum Shell
Previous: 3. Equation of Motion
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() functions,
functions,
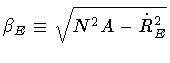 .
Evidently, the above definition is not unique. For instance, the choice of
the interval
.
Evidently, the above definition is not unique. For instance, the choice of
the interval