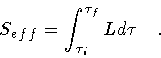Next: 3. Equation of Motion Up: Classical and Quantum Shell Previous:
1. Introduction
The dynamics of a generic system containing matter fields interacting
with gravity is encoded in the Einstein-Hilbert action
| S |
= |
Sg + Sm + SB |
|
| |
= |
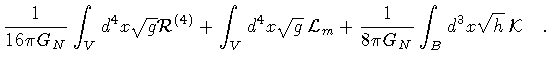 |
(3) |
The notation is as follows: GN stands for Newton's constant, g
is the determinant of the four dimensional spacetime metric,
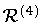 is the corresponding Ricci scalar,
is the corresponding Ricci scalar,
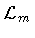 is the matter field Lagrangian density,
is the matter field Lagrangian density, 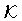 is the
extrinsic curvature of the three dimensional boundary, (B), of the
four-dimensional region V of integration, and h is the determinant of the
three-dimensional metric on the boundary. The presence
of the surface term allows the field equations to be
obtained from a variational principle in such a way that only
the metric on the boundary is held fixed.
is the
extrinsic curvature of the three dimensional boundary, (B), of the
four-dimensional region V of integration, and h is the determinant of the
three-dimensional metric on the boundary. The presence
of the surface term allows the field equations to be
obtained from a variational principle in such a way that only
the metric on the boundary is held fixed.
The actual physical system under consideration consists of
two static, spherically symmetric, spacetimes
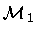 and
and
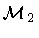 glued together along a time-like manifold
glued together along a time-like manifold
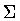 which represents the world history of the shell.
which represents the world history of the shell.
Our choice for
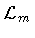 is
is
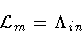 |
(4) |
in
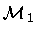 ,
,
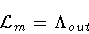 |
(5) |
in
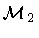 ,
and
,
and
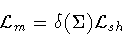 |
(6) |
along the shell, where
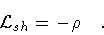 |
(7) |
As noted in Section I,
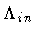 and
and
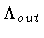 are the two
cosmological constants, and
are the two
cosmological constants, and 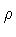 is the shell energy density.
Furthermore, one could easily extend the content of the
action integral by adding the electromagnetic term
is the shell energy density.
Furthermore, one could easily extend the content of the
action integral by adding the electromagnetic term
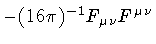 to
to
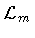 .
This addition would lead to the
Reissner-Nordström-de Sitter solution in
.
This addition would lead to the
Reissner-Nordström-de Sitter solution in
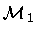 and
and
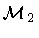 .
However, we shall not consider this case here, as
its discussion would only obscure the simplicity of the approach
that we wish to illustrate.
.
However, we shall not consider this case here, as
its discussion would only obscure the simplicity of the approach
that we wish to illustrate.
Solving Einstein's equations in
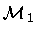 ,
we obtain the
Schwarzschild-de Sitter solution
,
we obtain the
Schwarzschild-de Sitter solution
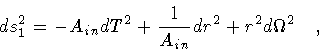 |
(8) |
where
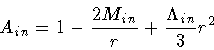 |
(9) |
and T, r, 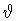 ,
,
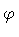 are the usual Schwarzschild coordinates.
Similarly, in
are the usual Schwarzschild coordinates.
Similarly, in
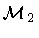
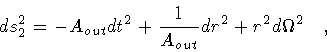 |
(10) |
where
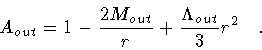 |
(11) |
The evolution of the shell, against this fixed background, is
described by the radius 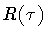 and by the lapse
and by the lapse 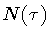 which characterize the shell intrinsic geometry according to equation
(2). This dynamics can be obtained by reducing the
action (3) to a functional depending
only on
which characterize the shell intrinsic geometry according to equation
(2). This dynamics can be obtained by reducing the
action (3) to a functional depending
only on 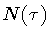 and
and 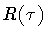 .
Our procedure of reduction follows
closely the discussion of ref.[7] (see also ref.[6]);
one element of novelty consists in the inclusion of the lapse function
.
Our procedure of reduction follows
closely the discussion of ref.[7] (see also ref.[6]);
one element of novelty consists in the inclusion of the lapse function
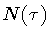 ,
which is essential to derive the Hamiltonian
constraint that one expects in a reparametrization invariant theory.
,
which is essential to derive the Hamiltonian
constraint that one expects in a reparametrization invariant theory.
To begin with, let us specify the volume V of integration. As shown in
fig.1, the volume is bounded by two space-like surfaces
T = T i and
T = T f, and by two time-like
surfaces:
r = R 1 and
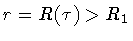 in
in
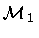 ,
and by
t = t i,
t = t f,
,
and by
t = t i,
t = t f,
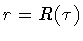 and
and
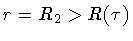 in
in
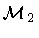 .
T1, t1, T2, t2, R1, R2
are constants. Furthermore, we assume, for the moment, that V lies in
a region of spacetime where the Killing vectors of the
metric (8-10),
.
T1, t1, T2, t2, R1, R2
are constants. Furthermore, we assume, for the moment, that V lies in
a region of spacetime where the Killing vectors of the
metric (8-10),
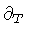 and
and
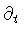 respectively, are both time-like. Later on, we shall
give a supplementary rule for the case in which the above condition
is not satisfied.
respectively, are both time-like. Later on, we shall
give a supplementary rule for the case in which the above condition
is not satisfied.
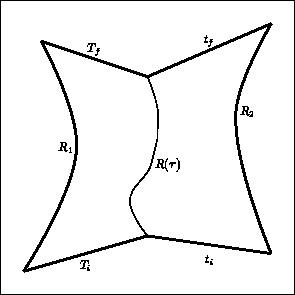
Figure:
Graphical representation of the integration volume with two
dimensions suppressed: Ti (Tf) and ti (tf) label the initial
(final) surfaces which are the space-like
boundaries of the integration volume. R1 and R2
represent the time-like boundaries, and 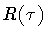 parametrizes the shell
radius which separates the interior domain
from the exterior one.
parametrizes the shell
radius which separates the interior domain
from the exterior one.
 |
Evaluating the induced metric on both side of the
shell, and comparing with eq.(2), we find the
implicit dependence of the Schwarzschild time variables on the parameter
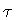 ,
,
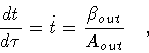 |
(12) |
where
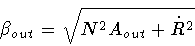 |
(13) |
and
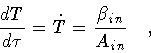 |
(14) |
where
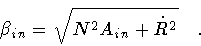 |
(15) |
Note that the 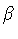 -functions defined above contain a sign
ambiguity[7], which is resolved by requiring that
-functions defined above contain a sign
ambiguity[7], which is resolved by requiring that 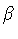 be
positive (negative) if the outer normal to
be
positive (negative) if the outer normal to
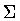 points toward increasing (decreasing) values of r.
points toward increasing (decreasing) values of r.
Our immediate objective, for the remainder of this section, is to
obtain the reduced form of the action integral, and we shall do so
by discussing each individual term separately. The explicit form of
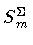 ,
the contribution of the shell to Sm, is given by
,
the contribution of the shell to Sm, is given by
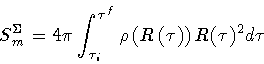 |
(16) |
supplemented by an equation of state relating the energy density
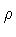 to the tangential pressure p. Such a relation is usually
obtained from the conservation equation for the shell stress-energy tensor,
to the tangential pressure p. Such a relation is usually
obtained from the conservation equation for the shell stress-energy tensor,
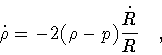 |
(17) |
and we shall discuss some simple special cases of this equation later on in
the text.
Next, in order to calculate
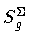 ,
the contribution
of the shell to Sg in the action integral, we first introduce Gaussian
normal coordinates near the shell
,
the contribution
of the shell to Sg in the action integral, we first introduce Gaussian
normal coordinates near the shell
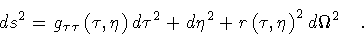 |
(18) |
As usual, the triplet (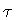 ,
,
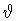 ,
,
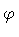 )
specifies a point on the shell, while
)
specifies a point on the shell, while 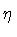 represents the geodesic
distance off the shell. One has
represents the geodesic
distance off the shell. One has 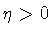 in
in
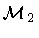 ,
and
,
and 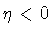 in
in
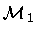 .
Furthermore,
.
Furthermore,
One can now start the evaluation of
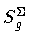 :
:
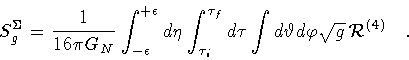 |
(21) |
Here 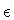 is an arbitrary small positive number, which at the end of
the calculation is set to zero. The Ricci scalar
is an arbitrary small positive number, which at the end of
the calculation is set to zero. The Ricci scalar
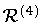 can be
expressed as
can be
expressed as
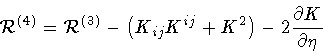 |
(22) |
where Kij stands for the extrinsic curvature of the
hyper-surface of constant 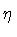 ,
and
,
and
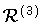 is the Ricci scalar constructed from the three-dimensional
metric g ij on the hyper-surface of constant
is the Ricci scalar constructed from the three-dimensional
metric g ij on the hyper-surface of constant 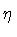 .
The relation between K ij and the normal derivative
of the three-metric is simply
.
The relation between K ij and the normal derivative
of the three-metric is simply
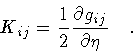 |
(23) |
Evaluating these quantities, one eventually obtains
and
All of the above leads to the following expression of
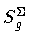
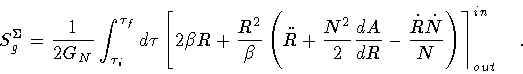 |
(28) |
In eq.(28) the notation
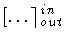 means, as usual,
means, as usual,
![$[ \dots ] \rceil _{in} - [ \dots ] \rceil _{out}$](img83.gif) .
.
The contributions of
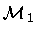 and
and
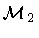 to Sg, which we denote by S1g and S2g
respectively, are easily evaluated since
to Sg, which we denote by S1g and S2g
respectively, are easily evaluated since
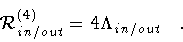 |
(29) |
This reduces the form of
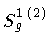 to a volume integral of the
same type as
to a volume integral of the
same type as
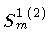 .
.
Finally, the surface term in the action integral, which eliminates
the second derivative term 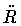 present in eq.(28),
can be written as
present in eq.(28),
can be written as
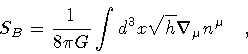 |
(30) |
where 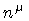 is the unit normal to the boundary three-surface,
and h is the determinant of the metric of the
three-surface. Again, following the same steps as in
ref.[7], one obtains
is the unit normal to the boundary three-surface,
and h is the determinant of the metric of the
three-surface. Again, following the same steps as in
ref.[7], one obtains
The end result of the above calculations is the following expression
of the action integral
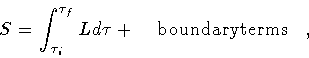 |
(32) |
where
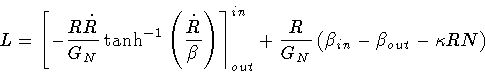 |
(33) |
and
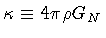 .
The additional ``boundary terms'' in eq.(32)
collectively refer to contributions which are simply proportional to
.
The additional ``boundary terms'' in eq.(32)
collectively refer to contributions which are simply proportional to
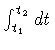 or
or
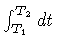 .
Their explicit form
is irrelevant for our purposes. Indeed, since the intrinsic dynamics of the
shell depends only on the interior and exterior geometry, both of
which are fixed, and not on the spacetime volume
V chosen, we define the shell effective
action by subtracting the boundary terms in
eq.(32) [6]. Therefore, the promised form
of the reduced, or effective, action is given by
.
Their explicit form
is irrelevant for our purposes. Indeed, since the intrinsic dynamics of the
shell depends only on the interior and exterior geometry, both of
which are fixed, and not on the spacetime volume
V chosen, we define the shell effective
action by subtracting the boundary terms in
eq.(32) [6]. Therefore, the promised form
of the reduced, or effective, action is given by
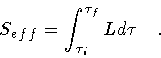 |
(34) |
As a consistency check, in the next section we shall verify that
varying this reduced action yields the Israel equation of motion
(1) for the shell.



Next: 3. Equation of Motion
Up: Classical and Quantum Shell
Previous: 1. Introduction
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
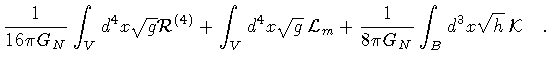
![]() and
and
![]() glued together along a time-like manifold
glued together along a time-like manifold
![]() which represents the world history of the shell.
which represents the world history of the shell.
![]() is
is
![]() ,
we obtain the
Schwarzschild-de Sitter solution
,
we obtain the
Schwarzschild-de Sitter solution
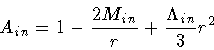
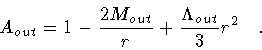
![]() in
in
![]() ,
and by
t = t i,
t = t f,
,
and by
t = t i,
t = t f,
![]() and
and
![]() in
in
![]() .
T1, t1, T2, t2, R1, R2
are constants. Furthermore, we assume, for the moment, that V lies in
a region of spacetime where the Killing vectors of the
metric (8-10),
.
T1, t1, T2, t2, R1, R2
are constants. Furthermore, we assume, for the moment, that V lies in
a region of spacetime where the Killing vectors of the
metric (8-10),
![]() and
and
![]() respectively, are both time-like. Later on, we shall
give a supplementary rule for the case in which the above condition
is not satisfied.
respectively, are both time-like. Later on, we shall
give a supplementary rule for the case in which the above condition
is not satisfied.

![]() ,
,
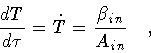
![]() ,
the contribution of the shell to Sm, is given by
,
the contribution of the shell to Sm, is given by
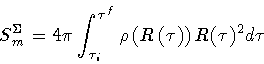
![]() ,
the contribution
of the shell to Sg in the action integral, we first introduce Gaussian
normal coordinates near the shell
,
the contribution
of the shell to Sg in the action integral, we first introduce Gaussian
normal coordinates near the shell
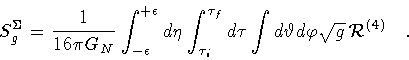
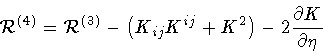
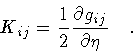
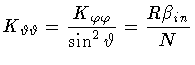
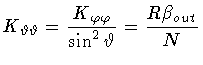
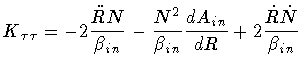
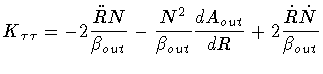
![]() and
and
![]() to Sg, which we denote by S1g and S2g
respectively, are easily evaluated since
to Sg, which we denote by S1g and S2g
respectively, are easily evaluated since
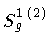 to a volume integral of the
same type as
to a volume integral of the
same type as
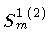 .
.
![]() present in eq.(28),
can be written as
present in eq.(28),
can be written as
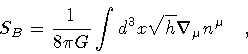
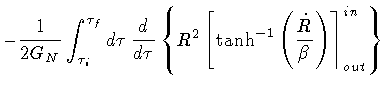

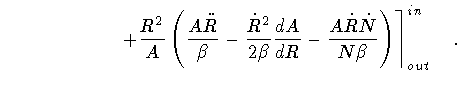
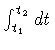 or
or
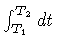 .
Their explicit form
is irrelevant for our purposes. Indeed, since the intrinsic dynamics of the
shell depends only on the interior and exterior geometry, both of
which are fixed, and not on the spacetime volume
V chosen, we define the shell effective
action by subtracting the boundary terms in
eq.(32) [6]. Therefore, the promised form
of the reduced, or effective, action is given by
.
Their explicit form
is irrelevant for our purposes. Indeed, since the intrinsic dynamics of the
shell depends only on the interior and exterior geometry, both of
which are fixed, and not on the spacetime volume
V chosen, we define the shell effective
action by subtracting the boundary terms in
eq.(32) [6]. Therefore, the promised form
of the reduced, or effective, action is given by