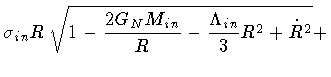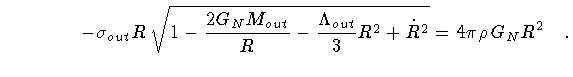1. Introduction

According to current ideas in cosmology, in particular the inflationary scenario [1], the universe would consist of (infinitely) many self reproducing bubbles which are continuously nucleated quantum mechanically. Some of them expand and look like a Friedmann universe, others collapse to form black holes and some are connected by wormholes.

In principle, this dynamical network may exist even at a very small scale of distances: at the Planck scale, it is expected to be the manifestation of gravitational fluctuations which induce a foam-like structure on the spacetime manifold [2]. A complete analysis of the global dynamics of this structure is difficult at present, as it involves the details of a quantum theory of gravity. From our vantage point, however, this complex structure can be approximated by an ensemble of cells of spacetime, each characterized by its own constant vacuum energy density and mass. In principle, each cell may behave as a black hole, wormhole or an inflationary bubble, depending on the matching conditions on the neighboring cells. One hopes, then, that some insight in the structure of the vacuum may be gained by examining a much simpler system consisting of a self gravitating thin shell separating two spherically symmetric domains of spacetime.

Following this line of thinking, black hole, wormhole and inflationary bubble models were constructed, and their dynamics was investigated in some detail ([3]-[9]) using the Israel matching condition between the internal and the external metric along the shell orbit in spacetime[10]:

 

$$\sigma _{in} R\, \sqrt{ 1 - \frac{2 G_N M _{in}}{R} - \frac{\Lambda _{in}}{3} R^2 + \dot{R} ^2 } +$$

$$\qquad \qquad - \sigma _{out} R\, \sqrt{ 1 - \frac{2 G_N M _{out}}{R} - \frac{\Lambda _{out}}{3} R^2 + \dot{R} ^2 } = 4 \pi \rho\, G_N R^2\quad .$$ (1)

In the above equation, $\Lambda _{in/out} = 8 \pi G _{N} \epsilon_{in/out}$ are the cosmological constants associated with the internal (in) and external (out) vacuum energy, M _in/out are the respective mass parameters, $\rho$ is the shell energy density, and R is the radius of the shell. As a matter of notation, a ``dot" means derivation with respect to the shell proper time, and $\sigma _{in} (\sigma _{out}) = + 1$ if R increases in the outward normal direction to the shell, while $\sigma _{in} (\sigma _{out}) = - 1$ if R decreases. Furthermore, in eq.(1) $\rho$ is understood as a function of R to be determined from the surface stress tensor conservation law, once an equation of state relating the surface energy density and the tension of the shell is assigned.

Against this classical background, there exist at least two effective methods to approach the quantum dynamics of the shell: i) by constructing, for each model, a specific Hamiltonian operator which leads to eq.(1) (or, to some squared version of it) [3,5], [9,11], or, ii) by extracting from the Einstein-Hilbert action for the whole spacetime a one degree of freedom reduced action which, under variation, gives eq.(1) [6,8,12].

This second approach seems more rigorous and less arbitrary than the first method, inasmuch as it relies on a well established action principle in order ``to run" the machinery of the Lagrangian formalism. However, one drawback common to both approaches is their dependence on the choice of the evolution parameter (internal, external, proper) with respect to which one labels the world history of the shell. The choice of time coordinate, in turn, affects the choice of a particular quantization scheme, leading, in general, to quantum theories which are not unitarily equivalent. In some cases, a particular choice of evolution parameter may even be inconsistent with the canonical quantization procedure, which is then abandoned in favor of Euclidean or path integral methods [7,8].

The root of the problem, it seems to us, is the lack of a dynamical formulation which is invariant under a general redefinition of time, and the natural way to enforce this invariance property is through an action principle, or lagrangian formalism, which encodes both the classical and quantum dynamics of the shell. On mathematical grounds, one then expects that the invariace under time reparametrization leads to a primary constraint in the corresponding Hamiltonian formulation, while on physical grounds, one must demand that the equations derived from it, be consistent with Israel's matching condition. It seems satisfying, therefore, that the above mathematical and physical requirements go hand in hand in our formulation, in the sense that the primary constraint originating from time reparametrization, automatically generates a (secondary) Hamiltonian constraint which, in a simple gauge, represents nothing but Israel's matching condition.

To summarize, then, the main purpose of this paper is to suggest a framework in which both the classical and quantum dynamics of a self gravitating spherical shell is discussed in terms of the canonical formalism of constrained systems. Thus we start from the Einstein-Hilbert action which includes the world-history of the shell and its boundary; then, by extending a procedure due to Farhi, Guth and Guven (FGG)[7], we extract from it a reduced action for the shell radial degree of freedom. The FGG-method is ``extended" in the sense that, while the metric of the background manifold is fixed, the dynamical variables for the shell are chosen to be the scale factor $R(\tau )$ together with the lapse function $N(\tau)$. These variables determine the form of the intrinsic metric on the shell

$$ds_{\Sigma}^2 = - N(\tau) ^2 d \tau ^2 + R(\tau) ^2 d \Omega ^2 \quad ,$$ (2)

where $d \Omega ^2$ represents the line element of the unit 2-sphere, and $\tau$ is an arbitrary time parameter along $\Sigma$, the shell orbit in spacetime. As discussed earlier on, we insist that any redefinition of that parameter should not affect the dynamical evolution of the shell. This requirement has rather far reaching mathematical and physical implications that we discuss in the following sections. Thus, in Section II, we define our system and obtain a reduced action for the shell. In Section III, we show how the matching equation (1) emerges as a Hamiltonian constraint reflecting the invariance of the theory under arbitrary $\tau$-reparametrization. In Section IV, we select a special gauge in order to explore the effective dynamics of the shell with an eye on the quantum discussion which follows in Section V. There we show that the Hamiltonian constraint, which led to Israel's equation in the classical theory, now leads to the Wheeler-DeWitt equation for the quantum states of the system. This is by no means accidental, since our formulation follows closely the minisuperspace approach to quantum cosmology, so that all classical and quantum shell-dynamics is encoded in the constraint that the Hamiltonian of the system vanishes in a weak sense. Section VI is devoted to an analytic and diagrammatic study of some quantum processes which are classically forbidden. The consistency of our formulation is then tested by deriving some well established results concerning vacuum decay. Section VII ends the paper with a summary of our discussion and some concluding remarks.

In order not to obscure the logical flow of our discussion, we have assembled several important technical steps into four Appendices. Appendix A clarifies the relationship between our variational procedure and the FGG-method; in Appendix B we show how to derive the general form of the Hamiltonian; in Appendix C we derive the general expression for the nucleation coefficient in vacuum decay by calculating its defining integral in the complex plane; finally, Appendix D provides all the necessary definitions and algebraic steps to connect our results about quantum tunneling with other results already existing in the literature.