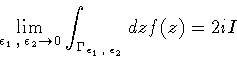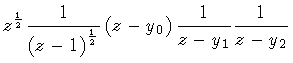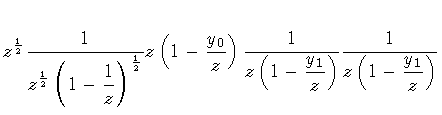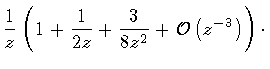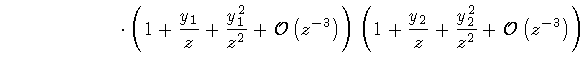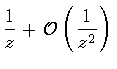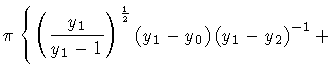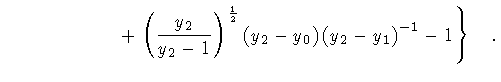Next: 11. Comparison with Parke Up: Classical and Quantum Shell Previous:
9. Hamiltonian for ,
10. Basic Integral for the de Sitter-de Sitter case.
The calculation of the integral (91) is performed
in the complex plane by considering the function
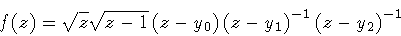 |
(127) |
which has two branch points (z=0 and z=1), and two simple
poles (z=y1 and z=y2). Accordingly, we integrate along the
path
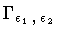 :
:
-
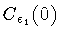 :
a clockwise circumference of radius
:
a clockwise circumference of radius
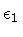 and center z=0;
and center z=0;
-
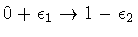 :
an oriented line segment of the x-axis in the
upper half of the complex plane;
:
an oriented line segment of the x-axis in the
upper half of the complex plane;
-
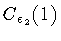 :
a clockwise circumference of radius
:
a clockwise circumference of radius
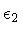 and center z=1;
and center z=1;
-
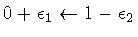 :
an oriented line segment of the x-axis in the
lower half of the complex plane
:
an oriented line segment of the x-axis in the
lower half of the complex plane
with
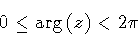 |
(128) |
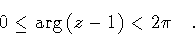 |
(129) |
Figure:
Integration path
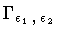 .
.
 |
Then, we have
![\begin{displaymath}
\lim _{\epsilon _1 \, , \: \epsilon _2 \to 0}
\int _{\Gamm...
...
{\cal R}{\rm {}es} \left\{ f , y_2 \right\}
\right]
\quad .
\end{displaymath}](img303.gif) |
(130) |
It is also true that
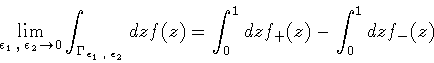 |
(131) |
with
Therefore,
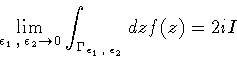 |
(134) |
with
![\begin{displaymath}I = \pi \left [
{\cal R}{\rm {}es} \left\{ f , +\infty \righ...
... {\cal R}{\rm {}es} \left\{ f , y_2 \right\}
\right ]
\quad .
\end{displaymath}](img310.gif) |
(135) |
The residue of the function at infinity is found from its
asymptotic expansion in powers of z-1:
The opposite of the coefficient of z -1 yields the result:
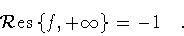 |
(137) |
Next, the residues at the poles
z=y1 , y2 are given by
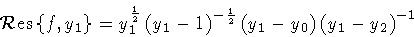 |
(138) |
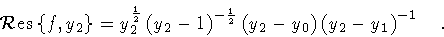 |
(139) |
Then, summing up our results, we finally obtain the expression of the
integral
| I |
= |
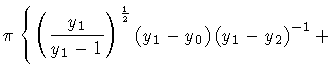 |
|
| |
|
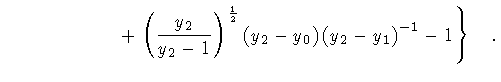 |
(140) |



Next: 11. Comparison with Parke Up: Classical and Quantum Shell Previous:
9. Hamiltonian for ,
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
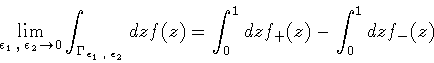
![$\displaystyle \left [ \vert z \vert \right ] ^{\frac{1}{2} }
\left [ \vert z - ...
...^{i \pi } \right ] ^{-1}
\left [ \vert z - y _2 \vert e^{i \pi } \right ] ^{-1}$](img306.gif)
![$\displaystyle \left [ \vert z \vert e^{2 i \pi } \right ] ^{\frac{1}{2} }
\left...
...^{i \pi } \right ] ^{-1}
\left [ \vert z - y _2 \vert e^{i \pi } \right ] ^{-1}$](img307.gif)