


Next: Bibliography Up: Classical and Quantum Shell Previous:
10. Basic Integral for
11. Comparison with Parke
Parke's result for the bounce action is[17]
![\begin{displaymath}B = B _0\, r \left [
\left(
\frac{\bar{\rho} _0}{2 \Lambda...
...) ^{2}
,
\frac{\Lambda ^{2}}{\lambda ^{2}}
\right ]
\quad ,
\end{displaymath}](img322.gif) |
(141) |
where
![\begin{displaymath}r \left [ x , y \right ]
=
\frac{
2 \left [ \left ( 1 + x ...
...)
\left( 1 + 2 x y + x ^{2} \right) ^{\frac{1}{2}}
}
\quad .
\end{displaymath}](img323.gif) |
(142) |
Moreover
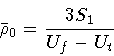 |
(143) |
is the critical radius in the absence of gravity, and
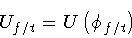 |
(144) |
represent the extremal points of the potential
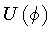 for the scalar field
for the scalar field 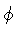 ,
which is minimally coupled to gravity; they
correspond to the false and true vacuum respectively.
The quantities
,
which is minimally coupled to gravity; they
correspond to the false and true vacuum respectively.
The quantities 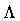 e
e 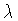 are related to these parameters
by the following relations7
are related to these parameters
by the following relations7
| |
|
![$\displaystyle \Lambda ^{2} = \left [
\frac{ 8 \pi \left( U _{f} - U _{t} \right)}{3}
\right ] ^{-1}$](img331.gif) |
(145) |
| |
|
![$\displaystyle \lambda ^{2} = \left [
\frac{ 8 \pi \left( U _{f} + U _{t} \right)}{3}
\right ] ^{-1}$](img332.gif) |
(146) |
and
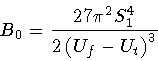 |
(147) |
represents the bounce action in the absence of gravity.
On the other hand, our result is
| |
|
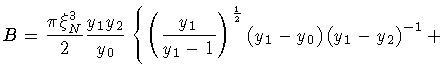 |
|
| |
|
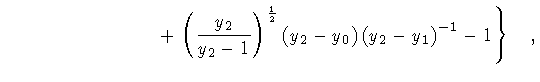 |
(148) |
in terms of the parameters defined in
eqs.(74-75)-(83)-(88-
90). The correspondence between our cosmological constants and the
false vacuum/true vacuum energies is given by the
relations:
| |
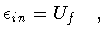 |
|
(149) |
| |
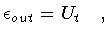 |
|
(150) |
with
| |
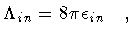 |
|
(151) |
| |
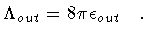 |
|
(152) |
Furthermore,
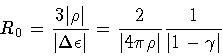 |
(153) |
corresponds to
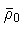 which, in turn, enables us to identify:
which, in turn, enables us to identify:
| |
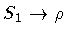 |
|
(154) |
| |
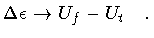 |
|
(155) |
Using this translation code, one can verify that Parke's expression for the
nucleation coefficient in the absence of gravity corresponds to
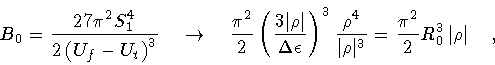 |
(156) |
which is exactly our result. Passing to the more general case, we note that:
| |
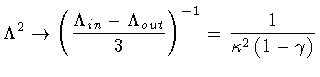 |
|
(157) |
| |
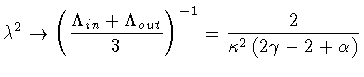 |
|
(158) |
from which we deduce,
| |
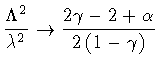 |
|
(159) |
| |
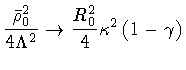 |
|
(160) |
and, as a consequence,
| |
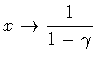 |
|
(161) |
| |
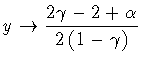 |
|
(162) |
| |
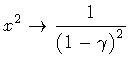 |
|
(163) |
| |
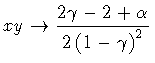 |
|
(164) |
| |
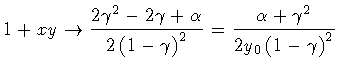 |
|
(165) |
| |
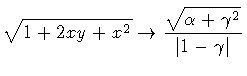 |
|
(166) |
| |
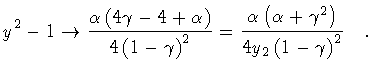 |
|
(167) |
Substituting all of the above in Eq.(141), we find
Next, we proceed in the same fashion with our own result. First, we have
| |
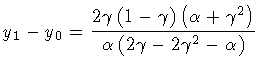 |
|
(169) |
| |
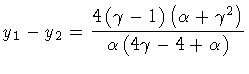 |
|
(170) |
| |
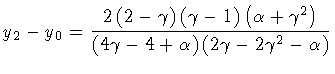 |
|
(171) |
| |
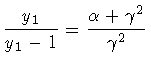 |
|
(172) |
| |
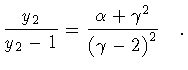 |
|
(173) |
Then, in the case in which
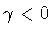 ,
or
,
or
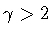 our expression for the nucleation coefficient becomes
our expression for the nucleation coefficient becomes
Finally, comparing the expressions
(168)-(174),
one sees that their equivalence is related to the equivalence of the terms
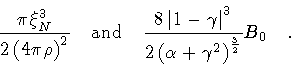 |
(175) |
However, in view of the equivalence between
eqs.(156) and (83), the only equality that needs to be
proved is that between
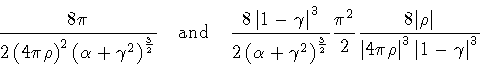 |
(176) |
which is trivially true.
In order to complete our discussion, we note that in the
case
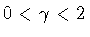 our result and that
of Parke do not coincide. The reason for this discrepancy may be
traced back to the fact that in the given interval of variation of
our result and that
of Parke do not coincide. The reason for this discrepancy may be
traced back to the fact that in the given interval of variation of
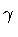 ,
one finds
,
one finds
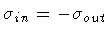 .
Therefore, as discussed in the text, the shell configuration
.
Therefore, as discussed in the text, the shell configuration
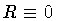 is no longer a classical solution so that no
quantum tunneling can occur in the first place.
is no longer a classical solution so that no
quantum tunneling can occur in the first place.



Next: Bibliography Up: Classical and Quantum Shell Previous:
10. Basic Integral for
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![\begin{displaymath}B = B _0\, r \left [
\left(
\frac{\bar{\rho} _0}{2 \Lambda...
...) ^{2}
,
\frac{\Lambda ^{2}}{\lambda ^{2}}
\right ]
\quad ,
\end{displaymath}](img322.gif)
![\begin{displaymath}r \left [ x , y \right ]
=
\frac{
2 \left [ \left ( 1 + x ...
...)
\left( 1 + 2 x y + x ^{2} \right) ^{\frac{1}{2}}
}
\quad .
\end{displaymath}](img323.gif)
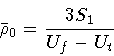
![$\displaystyle \Lambda ^{2} = \left [
\frac{ 8 \pi \left( U _{f} - U _{t} \right)}{3}
\right ] ^{-1}$](img331.gif)
![$\displaystyle \lambda ^{2} = \left [
\frac{ 8 \pi \left( U _{f} + U _{t} \right)}{3}
\right ] ^{-1}$](img332.gif)
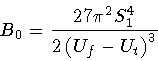
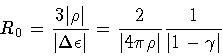
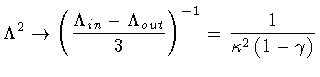
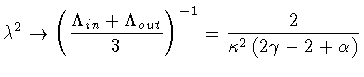
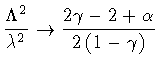
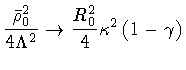
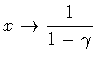
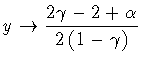
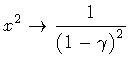
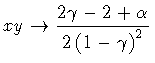
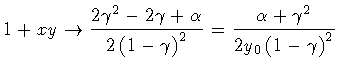
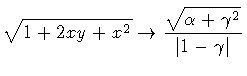
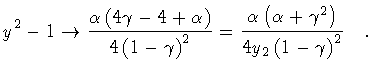
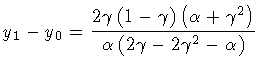
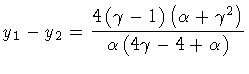
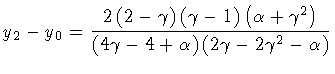
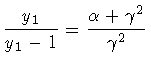
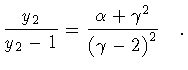
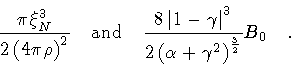
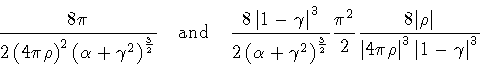
![]() our result and that
of Parke do not coincide. The reason for this discrepancy may be
traced back to the fact that in the given interval of variation of
our result and that
of Parke do not coincide. The reason for this discrepancy may be
traced back to the fact that in the given interval of variation of
![]() ,
one finds
,
one finds
![]() .
Therefore, as discussed in the text, the shell configuration
.
Therefore, as discussed in the text, the shell configuration
![]() is no longer a classical solution so that no
quantum tunneling can occur in the first place.
is no longer a classical solution so that no
quantum tunneling can occur in the first place.