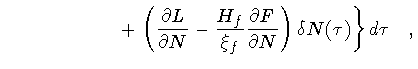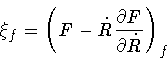Next: 9. Hamiltonian for , Up: Classical and Quantum Shell Previous:
7. Conclusion
8. The FGG-method and the Hamiltonian constraint
In this appendix we wish to discuss the
relationship between our variational procedure and the FGG-approach.
In this connection, it seems worth emphasizing that our
equations of motion were obtained by extremizing the action Seff
with respect to arbitrary variations of the functions  and
and  ,
vanishing at the end points, while the temporal boundary
was held fixed. This variational procedure is consistent with our
minisuperspace approach to
the intrinsic dynamics of the shell, according to which there should be
no reference to the internal, or external time coordinate,
or to the particular volume of integration chosen, since the latter
is just a convenient device to arrive at the equations
of motion for the shell. This represents a departure from the
FGG-method[7], which is based on a different
variational procedure. In that approach, the evolution of the shell is
parametrized by the external time, so that it seems
natural to consider variations in which the initial and
final external time ti and tf are held fixed. This, however, means
that
,
vanishing at the end points, while the temporal boundary
was held fixed. This variational procedure is consistent with our
minisuperspace approach to
the intrinsic dynamics of the shell, according to which there should be
no reference to the internal, or external time coordinate,
or to the particular volume of integration chosen, since the latter
is just a convenient device to arrive at the equations
of motion for the shell. This represents a departure from the
FGG-method[7], which is based on a different
variational procedure. In that approach, the evolution of the shell is
parametrized by the external time, so that it seems
natural to consider variations in which the initial and
final external time ti and tf are held fixed. This, however, means
that 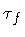 is not fixed, but varies according to
is not fixed, but varies according to
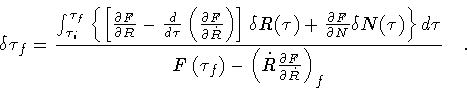 |
(100) |
This equation is obtained by taking the variation of
eq.(12)
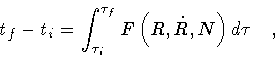 |
(101) |
where
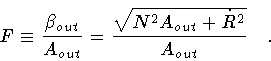 |
(102) |
Since now 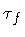 is not fixed, the variation of S eff
yelds additional contributions
is not fixed, the variation of S eff
yelds additional contributions
where
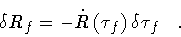 |
(104) |
Inserting eqs.(100) and (104)
into eq.(103), we obtain
where
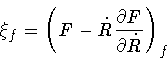 |
(106) |
and
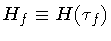 .
Demanding that
.
Demanding that 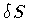 vanishes,
results now in the following equations of motion
vanishes,
results now in the following equations of motion
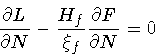 |
(107) |
![\begin{displaymath}\frac{\partial L}{\partial R}
-
\frac{d}{d \tau}
\left(
\...
...\partial F}{\partial \dot{R}}
\right)
\right]
=
0
\quad .
\end{displaymath}](img250.gif) |
(108) |
Now, Eq.(107) does not include an acceleration term; again,
it represents a constraint which can be rewritten as
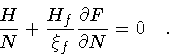 |
(109) |
Eq.(108), on the other hand, gives
![\begin{displaymath}\frac{d}{d\tau}
\left( \frac{H}{N} \right)
-
\frac{H_f}{\x...
...\partial F}{\partial \dot{R}}
\right)
\right]
=
0
\quad ,
\end{displaymath}](img252.gif) |
(110) |
so that the solution of both equations
(109-110) is H=0. In fact,
setting H=0 in eq.(109) we find Hf = 0,
which, once inserted in eq.(110), implies that
the Hamiltonian constraint H=0 is preserved in time, which is our result.



Next: 9. Hamiltonian for , Up: Classical and Quantum Shell Previous:
7. Conclusion
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() and
and ![]() ,
vanishing at the end points, while the temporal boundary
was held fixed. This variational procedure is consistent with our
minisuperspace approach to
the intrinsic dynamics of the shell, according to which there should be
no reference to the internal, or external time coordinate,
or to the particular volume of integration chosen, since the latter
is just a convenient device to arrive at the equations
of motion for the shell. This represents a departure from the
FGG-method[7], which is based on a different
variational procedure. In that approach, the evolution of the shell is
parametrized by the external time, so that it seems
natural to consider variations in which the initial and
final external time ti and tf are held fixed. This, however, means
that
,
vanishing at the end points, while the temporal boundary
was held fixed. This variational procedure is consistent with our
minisuperspace approach to
the intrinsic dynamics of the shell, according to which there should be
no reference to the internal, or external time coordinate,
or to the particular volume of integration chosen, since the latter
is just a convenient device to arrive at the equations
of motion for the shell. This represents a departure from the
FGG-method[7], which is based on a different
variational procedure. In that approach, the evolution of the shell is
parametrized by the external time, so that it seems
natural to consider variations in which the initial and
final external time ti and tf are held fixed. This, however, means
that ![]() is not fixed, but varies according to
is not fixed, but varies according to
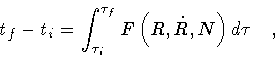
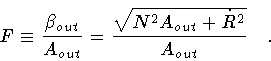
![$\displaystyle \int ^{\tau _f} _{\tau _i}
\left\{
\left[
\frac{\partial L}{\part...
...(
\frac{\partial f}{\partial \dot{R}}
\right)
\right]
\delta R(\tau)
\right .
+$](img244.gif)