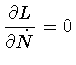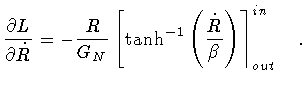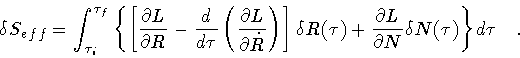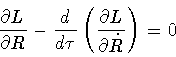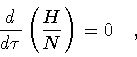Next: 4. Effective Dynamics Up: Classical and Quantum Shell Previous:
2. The Reduced Action.
The purpose of this section is twofold: i) to set up the
Hamiltonian formalism in preparation of the quantization procedure, and ii) to
show that the equations of motion of the shell are equivalent to the matching
condition (1). This section is supplemented by
Appendix
A in which we connect our canonical formalism
to the FGG-approach.
Presently, our first step is to define the conjugate momenta corresponding
to the dynamical variables N and R:
| PN |
= |
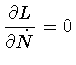 |
(35) |
| PR |
= |
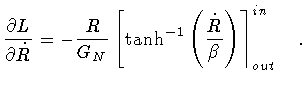 |
(36) |
From the above equations, we then obtain the form of the Hamiltonian for our
system
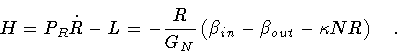 |
(37) |
Since L is independent of 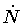 ,
it follows that the
corresponding conjugate momentum vanishes identically
(eq.(35)). That relation represents a primary
constraint which reflects the invariance of S eff under any
,
it follows that the
corresponding conjugate momentum vanishes identically
(eq.(35)). That relation represents a primary
constraint which reflects the invariance of S eff under any
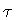 -reparametrization which maps the boundary (
-reparametrization which maps the boundary (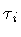 ,
,
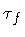 )
into
itself: for
)
into
itself: for
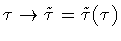 with
with
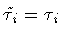
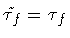 ,
we have
,
we have
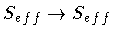 ,
as it is easily seen if one keeps in mind the
tensorial character of
N 2 = - g 00.
This primary constraint, in turn, generates a secondary constraint, namely
the vanishing of the Hamiltonian (37). Indeed, the
equations of motion of the shell are obtained by
requiring that S eff be stationary under variation of the functions
,
as it is easily seen if one keeps in mind the
tensorial character of
N 2 = - g 00.
This primary constraint, in turn, generates a secondary constraint, namely
the vanishing of the Hamiltonian (37). Indeed, the
equations of motion of the shell are obtained by
requiring that S eff be stationary under variation of the functions
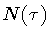 and
and 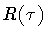 subject to the overall condition that they vanish at
the (fixed) boundaries
subject to the overall condition that they vanish at
the (fixed) boundaries
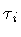 and
and 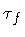 :
the variation of S eff gives
:
the variation of S eff gives
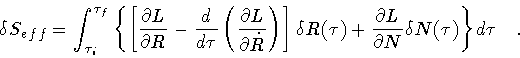 |
(38) |
Then, demanding that
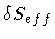 vanishes, yields two independent
relations. The first
vanishes, yields two independent
relations. The first
![\begin{displaymath}\frac{\partial L}{\partial N}
=
\frac{R}{G_N N} \left[ \bet...
...ta _{out} -
\kappa N R
\right]
=
- \frac{H}{N}
=
0
\quad
\end{displaymath}](img112.gif) |
(39) |
is not a true equation of motion, since 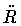 does not appear in it.
Rather, Eq.(39) represents a constraint
on the physically allowed states of our system, and since
does not appear in it.
Rather, Eq.(39) represents a constraint
on the physically allowed states of our system, and since
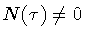 ,
it implies the (weakly) vanishing of the Hamiltonian
,
it implies the (weakly) vanishing of the Hamiltonian
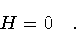 |
(40) |
On the other
hand, the second equation following from the requirement that
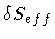 vanishes,
vanishes,
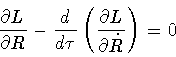 |
(41) |
can be rearranged in the form
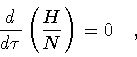 |
(42) |
which tells us, on account of eq.(40), that the
constraint H=0 is preserved in (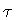 )
time, and that the lapse function
is completely arbitrary, as expected. As a matter of fact, all classical and
quantum evolution of the shell is encoded in the
Hamiltonian constraint (40). However, the dynamics of
the shell cannot be fully specified without fixing a gauge in our
reparametrization invariant formulation, and this invariance is
reflected in the arbitrariness of
)
time, and that the lapse function
is completely arbitrary, as expected. As a matter of fact, all classical and
quantum evolution of the shell is encoded in the
Hamiltonian constraint (40). However, the dynamics of
the shell cannot be fully specified without fixing a gauge in our
reparametrization invariant formulation, and this invariance is
reflected in the arbitrariness of 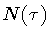 .
A natural choice is the gauge
.
A natural choice is the gauge
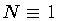 ,
which corresponds to selecting
,
which corresponds to selecting 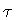 as proper time along the world history of the shell. In this gauge,
the constraint reads
as proper time along the world history of the shell. In this gauge,
the constraint reads
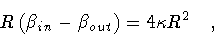 |
(43) |
which is just the matching
equation [10], now playing the role of a Hamiltonian
constraint describing the classical motion of the shell.



Next: 4. Effective Dynamics
Up: Classical and Quantum Shell
Previous: 2. The Reduced Action.
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY