


Next: Bibliography
Up: String Propagator: a Loop
Previous: 5.2 Integrating the path
The main results of this paper can be summarized as follows.
Starting with the canonical form of the Schild action for
a closed, bosonic string, it is possible to formulate the
Hamilton-Jacobi theory of string dynamics in loop space,
with the proper area of the string manifold playing the role
of evolution parameter. The conjugate dynamical quantity is an
area-Hamiltonian which is quadratic in the corresponding
momenta so that it is possible to extend to strings, indeed to
any p-brane, many of the results which are applicable to a
relativistic point particle.
The Feynman path integral for quantum strings is then
equivalent to the functional wave equation (29) which
was derived without
recourse to a lattice approximation. For the kernel
(42), the path integral, or the corresponding wave
equation can be solved exactly.
If, as it is normally done, one starts from a reparametrization
invariant path integral over the string coordinates, the corresponding
amplitude describes the propagation of strings with fixed ``energy''
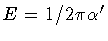 .
The relation between the two amplitudes is
given by equation (24).
.
The relation between the two amplitudes is
given by equation (24).
Three generalizations of the above results are almost
straightforward:
- 1.
- the wave equation for a closed string coupled to a Kalb-Ramond
field can be obtained from (29) through the replacement
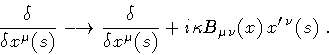 |
(48) |
Unfortunately, there is no straightforward way to solve the wave
equation, or to integrate the path integral, for an arbitrary
gauge potential;
- 2.
- some more work is required
to extend the above formalism to the case of a closed p-brane
imbedded into a D-dimensional spacetime. However,
no essential difficulties arise in treating higher dimensional
extended objects;
- 3.
- once the quantum mechanical propagator
is known, then one can second quantize the system. If we introduce
the string wave function
![$\Psi [ x (s) ]$](img125.gif) as an element of a functional
space of string states, then we can write (29) as
as an element of a functional
space of string states, then we can write (29) as
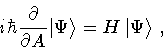 |
(49) |
where H is the area-hamiltonian operator.
Then, the corresponding Green function can be written as follows
![\begin{displaymath}G [ x (s) , x _{0} (s) ; m ^{2} ]
=
\frac{i}{\hbar}
\int _...
... \langle x(s) \vert \frac{1}{H} \vert x _{0} (s) \rangle
\ ,
\end{displaymath}](img127.gif) |
(50) |
or
![\begin{displaymath}G [ x (s) , x _{0} (s) ; m ^{2}]
=
\mathcal{N}
\int [D \Ps...
...s) ]
\exp \left( i S[\Psi ^{*} , \Psi ] / \hbar \right)
\ ,
\end{displaymath}](img128.gif) |
(51) |
where,
![$\Psi ^{*} [ x (s) ]$](img129.gif) ,
,
![$\Psi [ x _{0} (s) ]$](img130.gif) constitute a pair of
complex functional fields, and
constitute a pair of
complex functional fields, and
is the Marshall-Ramond [16] action for the dual string model.
Therefore, by extending the classical Hamilton-Jacobi formulation
of string dynamics into the quantum domain, one arrives at a
functional field theory in loop space.
As a final speculative
remark, it seems worth observing that the functional approach to the
quantum mechanics of strings is analogous, in several ways, to the
functional approach to quantum cosmology. For instance, the
`` wave function of the universe '' is defined in the functional space
of all possible 3-geometries, and we suggest that spatial loop
configurations in string theory play the same role as spatially
closed 3-geometries in quantum cosmology. Likewise, the
functional
Schrödinger equation for strings, at fixed areal-time,
plays the
same role as the Wheeler-DeWitt equation in quantum cosmology. If
this analogy is more than coincidental, then quantum string
theory in loop space may shed some light on the many dark areas of
quantum cosmology.



Next: Bibliography
Up: String Propagator: a Loop
Previous: 5.2 Integrating the path
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
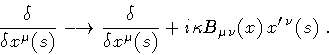
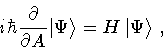
![\begin{displaymath}G [ x (s) , x _{0} (s) ; m ^{2} ]
=
\frac{i}{\hbar}
\int _...
... \langle x(s) \vert \frac{1}{H} \vert x _{0} (s) \rangle
\ ,
\end{displaymath}](img127.gif)
![\begin{displaymath}G [ x (s) , x _{0} (s) ; m ^{2}]
=
\mathcal{N}
\int [D \Ps...
...s) ]
\exp \left( i S[\Psi ^{*} , \Psi ] / \hbar \right)
\ ,
\end{displaymath}](img128.gif)
![$\displaystyle \int [D x ^{\mu} (s)] \,
\Psi ^{*} [ x (s) ]
\left[
-
\hbar ^{2}
\left(
\int _{0} ^{1} ds
\sqrt{x ^{\, \prime \, 2}}
\right) ^{-1}
\cdot
\right .$](img132.gif)
![$\displaystyle \qquad \qquad
\left .
\cdot
\int _{0} ^{1} \frac{ds}{\sqrt{x^{\, ...
...{2}}{\delta x ^{\mu} (s) \ \delta x _{\mu} (s)}
+
m ^{4}
\right]
\Psi [ x (s) ]$](img133.gif)