


Next: 5. Computing the kernel
Up: String Propagator: a Loop
Previous: 3. Feynman and Jacobi
4. The string kernel wave equation
The purpose of this section is to show how to derive
the functional wave equation for
K [ x (s) , x 0 (s) ; A] from the
corresponding path integral.
This equation describes how the string responds to a
variation of the final boundary
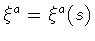 ,
just as the
ordinary Schrödinger equation describes a particle reaction
to a shift of the time interval end-point. As we have seen
in section 2,
the string ``natural'' evolution parameter is the area A of
the string manifold, so that functional or area derivatives
generate
``translations'' in loop space, or string deformations in
Minkowski space. Thus, we expect the functional wave
equation to be of order one in
,
just as the
ordinary Schrödinger equation describes a particle reaction
to a shift of the time interval end-point. As we have seen
in section 2,
the string ``natural'' evolution parameter is the area A of
the string manifold, so that functional or area derivatives
generate
``translations'' in loop space, or string deformations in
Minkowski space. Thus, we expect the functional wave
equation to be of order one in
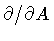 ,
and of
order two in
,
and of
order two in
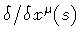 ,
or
,
or
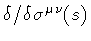 5.
5.
The standard procedure to arrive at the kernel wave equation
goes through a recurrence relation satisfied by the
discretized version of the Jacobi path integral
[14], [15]. However, such a construction is well
defined only when the action is a polynomial in the dynamical
variables. For a non-linear action such
as the Nambu-Goto area functional, a lattice definition of the path
integral is much less obvious. Moreover,
the continuum functional wave equation is
recovered through the highly non-trivial limit of vanishing
lattice step [14], [15]. In any case,
the whole procedure seems disconnected from the classical
approach to string dynamics, whereas we would like to see a logical
continuity between quantum and classical dynamics. Against this
background, it seems useful to offer an alternative
path integral derivation of the string functional wave equation
which is deeply rooted in the
Hamiltonian formulation of string dynamics discussed in
section 2, and is basically derived from the same Jacobi
variational principle which we have consistently adopted so far.
The kernel variation under infinitesimal deformations of the
field variables is
![\begin{displaymath}\delta K [ x (s) , x _{0} (s) ; A]
=
\frac{i}{\hbar}
\int ...
...(\sigma)] \,
\delta S
\exp \left( {i S / \hbar} \right)
\ .
\end{displaymath}](img78.gif) |
(25) |
As usual, only boundary variations will contribute to
equation (25) if we restrict the fields to vary
within the family
of classical solutions corresponding to a given initial string
configuration. Then,
![\begin{displaymath}\delta S _{\mathrm{cl.}}[ C ; A ]
=
\oint _{C}
p _{\mu \nu} \,
\delta x ^{\mu} (s) \,
d x ^{\nu}
-
E \,
dA
\ .
\end{displaymath}](img79.gif) |
(26) |
From equations (25) and (26), we obtain
Then, by comparison of (27), (28) and
(10), one obtains immediately the kernel wave
equation
| |
|
![$\displaystyle -
\frac{\hbar ^{2}}{2 m ^{2}}
\left(
\int _{0} ^{1} ds
\sqrt{x ^{...
...{2}}
{\delta x ^{\mu} (s) \ \delta x _{\mu} (s)}
K [ x (s) , x _{0} (s) ; A ]
=$](img84.gif) |
|
| |
|
![$\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad
=
i
\hbar
\frac{\partial}{\partial A}
K [ x (s) , x _{0} (s) ; A]
.$](img85.gif) |
(29) |
Thus,
K [ x (s) , x 0 (s) ; A] can be determined either by solving
the functional wave equation (29), or by evaluating the path
integral (17).
Once equation (29) is given, it is straightforward to
show that
G[ C , C 0 ; m 2] satisfies the following equation
![\begin{displaymath}\left[
-
\hbar ^{2}
\left(
\int _{0} ^{1} \! \! \! ds
\s...
...ight]
G[ C , C _{0} ; m ^{2} ]
=
-
\delta [ C - C _{0}]
.
\end{displaymath}](img86.gif) |
(30) |
Therefore,
G[ C , C 0 ; m 2]
can be identified with the Green function for the string.



Next: 5. Computing the kernel
Up: String Propagator: a Loop
Previous: 3. Feynman and Jacobi
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![\begin{displaymath}\delta K [ x (s) , x _{0} (s) ; A]
=
\frac{i}{\hbar}
\int ...
...(\sigma)] \,
\delta S
\exp \left( {i S / \hbar} \right)
\ .
\end{displaymath}](img78.gif)
![\begin{displaymath}\delta S _{\mathrm{cl.}}[ C ; A ]
=
\oint _{C}
p _{\mu \nu} \,
\delta x ^{\mu} (s) \,
d x ^{\nu}
-
E \,
dA
\ .
\end{displaymath}](img79.gif)
![$\displaystyle \frac{\partial}{\partial A}
K [ x (s) , x _{0} (s) ; A ]$](img80.gif)
![$\displaystyle -
\frac{i E}{\hbar}
K [ x (s) , x _{0} (s) ; A]
\ ,$](img81.gif)
![$\displaystyle \frac{\delta}{\delta x ^{\mu} (s)}
K [ x (s) , x _{0} (s) ; A ]$](img82.gif)
![$\displaystyle \frac{i}{\hbar}
\int _{x _{0} (s)} ^{x(s)}
\int _{\xi _{0} (s)} ^...
...sigma)]
p _{\mu \nu} x^{\, \prime \, \nu}
\exp
\left( {i S / \hbar} \right) \ .$](img83.gif)
![$\displaystyle -
\frac{\hbar ^{2}}{2 m ^{2}}
\left(
\int _{0} ^{1} ds
\sqrt{x ^{...
...{2}}
{\delta x ^{\mu} (s) \ \delta x _{\mu} (s)}
K [ x (s) , x _{0} (s) ; A ]
=$](img84.gif)
![$\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad
=
i
\hbar
\frac{\partial}{\partial A}
K [ x (s) , x _{0} (s) ; A]
.$](img85.gif)
![\begin{displaymath}\left[
-
\hbar ^{2}
\left(
\int _{0} ^{1} \! \! \! ds
\s...
...ight]
G[ C , C _{0} ; m ^{2} ]
=
-
\delta [ C - C _{0}]
.
\end{displaymath}](img86.gif)