


Next: 4. The string kernel
Up: String Propagator: a Loop
Previous: 2. Functional Jacobi equation
3. Feynman and Jacobi path integrals
The path integral approach to string-dynamics is not only a
useful check of the
quantization procedure, but gives a new insight into
the quantum theory itself. In particular, it gives a better
insight into the
meaning of the equivalence between the Nambu-Goto action and the
Schild action. Furthermore,
it provides a physically transparent relationship between the
Feynman ``sum over histories'' integral and the Jacobi path
integral. However, to see how this comes about, one must keep in
mind that the momenta
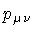 and
and 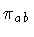 cannot vary freely, because
cannot vary freely, because 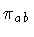 is
merely a shorthand notation for the function
is
merely a shorthand notation for the function
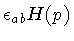 ,
and thus must satisfy the constraint equation
,
and thus must satisfy the constraint equation
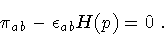 |
(13) |
This constraint may be incorporated in the action (3)
by means of a Lagrange multiplier
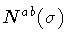
| |
|
![$\displaystyle S [ x (\sigma) , p (\sigma) , \xi (\sigma) , N (\sigma) ; A]
=
\frac{1}{2}
\int _{X ( \sigma )}
p _{\mu \nu} d x ^{\mu} \wedge d x ^{\nu}
+$](img49.gif) |
|
| |
|
![$\displaystyle \qquad \qquad +
\frac{1}{2}
\int _{\xi (\sigma)}
\pi _{ab} d \xi ...
...{2} \sigma
N ^{ab} (\sigma)
\left[
\pi _{ab}
-
\epsilon _{ab}
H (p)
\right]
\ ,$](img50.gif) |
(14) |
and its physical meaning can be read out of the classical
equation of motion obtained by varying 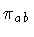 :
:
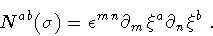 |
(15) |
Thus, N ab is the transformed 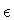 -tensor in the
new coordinate system. Then, apart from an over all
normalization
constant 4, the amplitude
for the initial string C 0 to ``evolve'' into the final
string C in a lapse of ``time A'', can be represented by the
path integral
-tensor in the
new coordinate system. Then, apart from an over all
normalization
constant 4, the amplitude
for the initial string C 0 to ``evolve'' into the final
string C in a lapse of ``time A'', can be represented by the
path integral
| |
|
![$\displaystyle K [ x (s) , x _{0} (s) ; A ]
=
\int _{ x _{0} (s)} ^{x (s)}
\int ...
...(s)} ^{\xi (s)} [D \mu (\sigma)]
e ^{i S [ x , p , \xi , \pi , N ; A ] / \hbar}$](img54.gif) |
|
| |
|
![$\displaystyle [D \mu (\sigma)]
\equiv
[D x ^{\mu} (\sigma)]
[D \xi ^{a} (\sigma)]
[D p _{\mu \nu} (\sigma)]
[D \pi _{ab} (\sigma)]
[D N _{cd} (\sigma)]
\ .$](img55.gif) |
(17) |
At the classical level, H, or 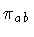 ,
is independent of
the coordinates
,
is independent of
the coordinates
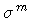 because of the balance equation
(4). The
same result is obtained at the quantum level by integrating
out the
because of the balance equation
(4). The
same result is obtained at the quantum level by integrating
out the
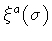 fields:
fields:
| |
|
![$\displaystyle \int _{\xi _{0} (s)} ^{\xi (s)} [D \xi ^{a} (\sigma)]
\exp
\left\...
...\hbar}
\int _{\xi (\sigma)} d \xi ^{a} \wedge d\xi ^{b}
\,
\pi _{ab}
\right\}
=$](img57.gif) |
|
| |
|
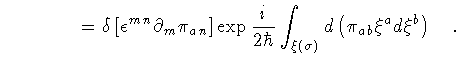 |
(18) |
The functional Dirac-delta requires 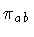 to satisfy the
classical equation of motion, i.e.
to satisfy the
classical equation of motion, i.e.
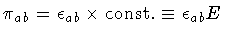 .
Therefore,
.
Therefore,
| |
|
![$\displaystyle \int \! [D \pi _{ab}]
\delta
\left[
\epsilon ^{mn}
\partial _{m} ...
... _{\Sigma} \! \! \! d ^{2} \sigma
N ^{ab} (\sigma) \pi _{ab}
\right]
\right\}
=$](img60.gif) |
|
| |
|
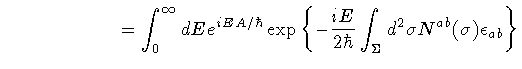 |
(19) |
where we have assumed that the Hamiltonian is bounded from
below and is normalized in such a way that 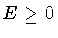 .
Then, the Feynman path integral can be written as follows
.
Then, the Feynman path integral can be written as follows
where we have introduced the Jacobi path integral
G[ C , C 0 ; E]
as the amplitude for a string to propagate from C 0 to
C, at fixed energy E.
The most important property of
G[ C , C 0 ; E] is reparametrization invariance.
If we integrate out the area momentum
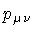 ,
we obtain
,
we obtain
| G[ C , C 0 ; E ] |
|
![$\displaystyle =
\int _{x _{0} (s)} ^{x (s)} [D x ^{\mu} (\sigma)][D N (\sigma)]
\times$](img66.gif) |
|
| |
|
![$\displaystyle \qquad \qquad \qquad \times
\exp
\left\{
-
\frac{i}{\hbar}
\int _...
...rac{m ^{2}}{4 N}
{\dot{x}}^{\mu \nu} {\dot{x}}_{\mu \nu}
+
N E
\right]
\right\}$](img67.gif) |
(21) |
where
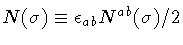 .
.
Equation (21)
is manifestly invariant under reparametrization
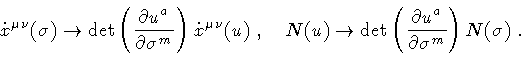 |
(22) |
Finally, if we estimate the path integral (21) around the
saddle point
 ,
we find
,
we find
![\begin{displaymath}G[ C , C _{0} ; E ]
=
\int _{ x _{0} (s)} ^{x (s)} [ D x ^{...
...sqrt{- {\dot{x}}^{\mu \nu} {\dot{x}}_{\mu \nu}}
\right\}
\ ,
\end{displaymath}](img71.gif) |
(23) |
which is the usual path integral weighed by the
Nambu-Goto action, once we fix
E = m 2 / 2.
The result (23) suggests the following concluding
remarks for this section:
- 1.
- equation (23) could be assumed at the outset and
taken as a starting
point for string quantization by means of functional
techniques. The advantage of our derivation is that it clarifies the
physical meaning of such a
reparametrization invariant path integral:
it represents the string propagation amplitude at fixed
``area-energy''
 .
.
- 2.
- We can invert the Fourier transform (20)
and define
the reparametrization invariant path integral in terms of the
Feynman propagation amplitude at fixed ``area-lapse'' A
![\begin{displaymath}G[ C , C _{0} ; m ^{2} ]
\equiv
\frac{1}{2 i \hbar m ^{2}}
...
...
e ^{- i m ^{2} A / 2 \hbar} K[ x (s) , x _{0} (s) ; A]
\ .
\end{displaymath}](img72.gif) |
(24) |
Then, reparametrization offers an alternative definition of the
sum over histories: first, sum over all world-sheets of fixed area;
then, integrate over all possible values of the world-sheet area.
- 3.
- Equation (20) represents the quantum counterpart of the
classical equivalence [5] between the Nambu-Goto action
and the Schild action.



Next: 4. The string kernel
Up: String Propagator: a Loop
Previous: 2. Functional Jacobi equation
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() and
and ![]() cannot vary freely, because
cannot vary freely, because ![]() is
merely a shorthand notation for the function
is
merely a shorthand notation for the function
![]() ,
and thus must satisfy the constraint equation
,
and thus must satisfy the constraint equation
![$\displaystyle S [ x (\sigma) , p (\sigma) , \xi (\sigma) , N (\sigma) ; A]
=
\frac{1}{2}
\int _{X ( \sigma )}
p _{\mu \nu} d x ^{\mu} \wedge d x ^{\nu}
+$](img49.gif)
![$\displaystyle \qquad \qquad +
\frac{1}{2}
\int _{\xi (\sigma)}
\pi _{ab} d \xi ...
...{2} \sigma
N ^{ab} (\sigma)
\left[
\pi _{ab}
-
\epsilon _{ab}
H (p)
\right]
\ ,$](img50.gif)
![$\displaystyle \int \! [D \pi _{ab}]
\delta
\left[
\epsilon ^{mn}
\partial _{m} ...
... _{\Sigma} \! \! \! d ^{2} \sigma
N ^{ab} (\sigma) \pi _{ab}
\right]
\right\}
=$](img60.gif)
![]() ,
we obtain
,
we obtain
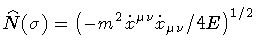 ,
we find
,
we find