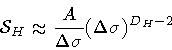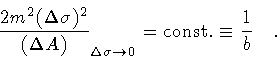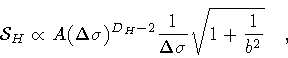Next: 5. Conclusions, some final
Up: 4. Fractal Strings
Previous: 4.1 The Hausdorf dimension
4.2 Classical-to-fractal geometric transition
The role of area resolution, as pointed out in the previous sections,
leads us to search for a critical area characterizing the transition
from classical to fractal geometry of the string stack.
To this end, we consider tha case in which the string possesses a non
vanishing average momentum, in which case we may use a
gaussian wave packet of the form (27).
The corresponding wave functional, in the  -representation, is
-representation, is
| |
|
![$\displaystyle \Psi _{K} (C ; A)
=
\frac{[ (\Delta \sigma) ^{2} / 2 \pi] ^{3/4}}
{[ (\Delta \sigma) ^{2} + i A / 2 m ^{2}] ^{3/2}}
\cdot$](img128.gif) |
|
| |
|
![$\displaystyle \quad \cdot
\exp
\left[
-
\frac{
\left(
\sigma ^{\mu \nu} \sigma ...
... \nu} / 4 m ^{2}
\right)
}
{2 [ (\Delta \sigma) ^{2} + i A / 2 m ^{2}]}
\right]$](img129.gif) |
(44) |
where we have used equation (34) to exchange
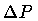 with
with
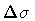 .
The corresponding probability density ``evolves'' as follows
.
The corresponding probability density ``evolves'' as follows
| |
|
![$\displaystyle \vert \Psi _{K} (C ; A) \vert ^{2}
=
\frac{(2 \pi) ^{-3/2}}
{
[
(\Delta \sigma) ^{2}
+
A ^{2} / 4 (\Delta\sigma) ^{2} m ^{4}
] ^{3/2}
}
\cdot$](img130.gif) |
|
| |
|
![$\displaystyle \qquad \qquad \qquad \qquad \cdot
\exp
\left[
-
\frac{
\left(
\si...
...\sigma) ^{2}
+
A ^ {2} / 4 (\Delta \sigma) ^{2} m ^{4}
\right]}
\right]
\quad .$](img131.gif) |
(45) |
Therefore, the average area variation
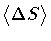 ,
when the loop wave packet drifts with a momentum
,
when the loop wave packet drifts with a momentum
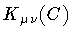 ,
is
,
is
![\begin{displaymath}\langle \Delta S \rangle
\equiv
\left[
\int [ {\mathcal{D}...
...(C)
\vert \Psi _{K} (C ; \Delta A) \vert ^{2}
\right] ^{1/2}
\end{displaymath}](img132.gif) |
(46) |
For our purpose, there is no need to compute the exact
form of the mean value (46), but only its dependence on
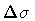 .
This can be done in three steps:
.
This can be done in three steps:
- 1.
- introduce the adimensional integration variable
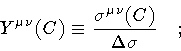 |
(47) |
- 2.
- shift the new integration variable as follows
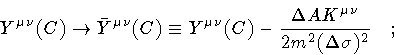 |
(48) |
- 3.
- rescale the integration variable as
![\begin{displaymath}\bar{Y}^{\mu \nu} (C)
\rightarrow
Z ^{\mu \nu} (C)
\equiv
...
...) ^{2}}{4 m ^{4} (\Delta \sigma) ^4}
\right] ^{1/2}
\quad .
\end{displaymath}](img135.gif) |
(49) |
Then, we obtain
where,
The parameter 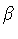 measures the ratio of the ``temporal'' to ``spatial''
uncertainty, while the area
measures the ratio of the ``temporal'' to ``spatial''
uncertainty, while the area
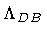 sets the scale of the
surface variation at which the string momentum is
sets the scale of the
surface variation at which the string momentum is
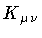 .
Therefore, always with the particle analogy in mind,
we shall call
.
Therefore, always with the particle analogy in mind,
we shall call
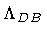 the loop DeBroglie area.
Let us assume, for the moment, that
the loop DeBroglie area.
Let us assume, for the moment, that 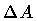 is
independent of
is
independent of
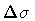 ,
so that either quantity can be
treated as a free parameter in the theory. A notable exception to this
hypothesis will be discussed shortly. Presently, we note that
taking the limit
,
so that either quantity can be
treated as a free parameter in the theory. A notable exception to this
hypothesis will be discussed shortly. Presently, we note that
taking the limit
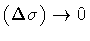 ,
affects only the first
term of the integral (50), and that its weight with respect
to the second term is measured by the ratio
,
affects only the first
term of the integral (50), and that its weight with respect
to the second term is measured by the ratio
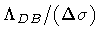 .
If the area resolution is much
larger than the loop DeBroglie area, then the first term is negligible:
.
If the area resolution is much
larger than the loop DeBroglie area, then the first term is negligible:
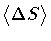 is independent of
is independent of
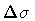 and
and
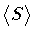 scales as
scales as
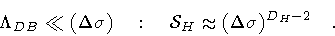 |
(53) |
In this case, independence of
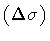 is achieved by
assigning
D H = 2.
As one might have anticipated, the detecting apparatus is
unable to resolve the graininess of the string stack, which
therefore appears as a smooth two dimensional surface.
is achieved by
assigning
D H = 2.
As one might have anticipated, the detecting apparatus is
unable to resolve the graininess of the string stack, which
therefore appears as a smooth two dimensional surface.
The fractal, or quantum, behavior manifests itself below
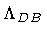 ,
when the first term in (50) provides the
leading contribution
,
when the first term in (50) provides the
leading contribution
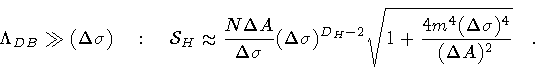 |
(54) |
This expression is less transparent than the relation (53),
as it involves also the 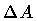 resolution. However, one may now consider
two special subcases in which the Hausdorff dimension can be
assigned a definite value.
resolution. However, one may now consider
two special subcases in which the Hausdorff dimension can be
assigned a definite value.
In the first case, we keep 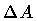 fixed, and scale
fixed, and scale
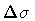 down to zero. Then, each
down to zero. Then, each
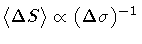 diverges,
because of larger and larger shape fluctuations, and
diverges,
because of larger and larger shape fluctuations, and
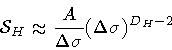 |
(55) |
requires
D H = 3.
The same result can be obtained also in the second subcase, in
which both
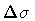 and
and 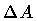 scale down to zero,
but in such a way that their ratio remains constant,
scale down to zero,
but in such a way that their ratio remains constant,
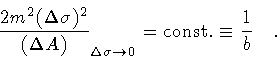 |
(56) |
The total interior area
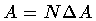 is kept fixed. Therefore, as
is kept fixed. Therefore, as
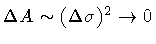 ,
then
,
then
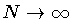 in order to keep A finite. Then,
in order to keep A finite. Then,
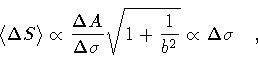 |
(57) |
and
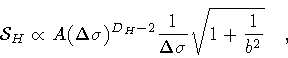 |
(58) |
which leads to
D H = 3 again. In the language of fractal
geometry, this interesting subcase corresponds to
self-similarity. Thus, the condition (57) defines
a special class of self-similar loops characterized by
an average area variation which is proportional to
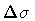 at any scale.
at any scale.



Next: 5. Conclusions, some final
Up: 4. Fractal Strings
Previous: 4.1 The Hausdorf dimension
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() -representation, is
-representation, is
![$\displaystyle \Psi _{K} (C ; A)
=
\frac{[ (\Delta \sigma) ^{2} / 2 \pi] ^{3/4}}
{[ (\Delta \sigma) ^{2} + i A / 2 m ^{2}] ^{3/2}}
\cdot$](img128.gif)
![$\displaystyle \quad \cdot
\exp
\left[
-
\frac{
\left(
\sigma ^{\mu \nu} \sigma ...
... \nu} / 4 m ^{2}
\right)
}
{2 [ (\Delta \sigma) ^{2} + i A / 2 m ^{2}]}
\right]$](img129.gif)
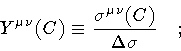
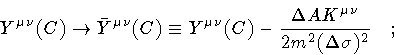
![\begin{displaymath}\bar{Y}^{\mu \nu} (C)
\rightarrow
Z ^{\mu \nu} (C)
\equiv
...
...) ^{2}}{4 m ^{4} (\Delta \sigma) ^4}
\right] ^{1/2}
\quad .
\end{displaymath}](img135.gif)