


Next: Bibliography
Up: Hausdorff Dimension of a
Previous: 4.2 Classical-to-fractal geometric transition
5. Conclusions, some final remarks, and outlook
Classical string dynamics is based on the simple and intuitive notion
that the world-sheet of a relativistic string consists of a
smooth, two-dimensional manifold embedded in a preexisting
spacetime. Switching from classical to quantum
dynamics changes this picture in a fundamental way. In the
path integral approach to particle quantum mechanics, Feynman and
Hibbs were first to point out that the trajectory of a particle is
continuous but nowhere differentiable [7]. This is because,
according to Heisenberg's principle, when a particle is more and more
precisely located in space, its trajectory becomes more and more
erratic. Abbott and Wise were next to point out that a particle
trajectory, appearing as a smooth line of topological
dimension one, turns into a fractal object of
Hausdorff dimension two, when the
resolution of the detecting apparatus is smaller than the particle
DeBroglie wavelength [8]. Likewise, extending the
path integral approach to the string case, one must take into account
the coherent contributions from all
the world-sheets satisfying some preassigned boundary
conditions, and one might expect that a string quantum world-sheet
is a fractal, non-differentiable surface. However, to give a
quantitative support to this expectation is less immediate than it
might appear at first glance. From an intuitive point of view, each
string bit can be localized only with a finite resolution
in position and momentum. Thus, a string loses its classical,
well defined geometric shape, and its world-sheet appears fuzzy as a
consequence of quantum fluctuations. However, the notion of a string
world-sheet is fully relativistic, and the implementation
of fractal geometry in high energy physics is an open field of
research with many aspects of it still under discussion [9].
In this paper, we have argued that it is advantageous to
work with a first quantized formulation of string dynamics.
The canonical quantization approach consists in
Fourier analyzing the string vibrations around an equilibrium
configuration and assign
the Fourier coefficients the role of ladder operators creating
and annihilating infinitely many vibration modes. Based on
our previous work [2], [3], we have suggested an
alternative view of a closed string quantum vibrations,
and we readily admit that the exact relationship between the
two quantization schemes is unclear and requires a more
exhaustive investigation. However, the conceptual difference
between the two approaches is sharp: we are quantizing the
string motion not through the displacement of each point on
the string, but through the string shape. The outcome
of this novel approach is a quantum mechanics of loops,
whose spacetime interpretation involves
quantum shape shifting transitions, i.e.,
quantum mechanical jumps among all possible string geometric
shapes. The emphasis on string shapes, rather than points,
represents a departure from the canonical formulation and
requires an appropriate choice of dynamical variables, namely, the
string configuration tensor 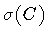 ,
and the areal time A.
This functional approach enables us to extend the quantum mechanical
discussion by Abbott and Wise to the case of a
relativistic (closed) string. It may seem somewhat
confusing, if not contradictory, that we deal with a relativistic system
in a quantum mechanical, i.e., non relativistic framework, as opposed to a
quantum field theoretical framework [10]. However, this is not
new in theoretical physics [11]. In any case, one has to
realize that there are two distinct levels of discussion in our approach.
At the spacetime level, where the actual deformations
in the string shape take place, the formulation is fully relativistic, as
witnessed by the covariant structure of our equations with
respect to the Lorentzian indices. However, at the loop space level,
where each ``point'' is representative of a particular loop
configuration, our formulation is quantum mechanical, in the sense that the
string coordinates
,
and the areal time A.
This functional approach enables us to extend the quantum mechanical
discussion by Abbott and Wise to the case of a
relativistic (closed) string. It may seem somewhat
confusing, if not contradictory, that we deal with a relativistic system
in a quantum mechanical, i.e., non relativistic framework, as opposed to a
quantum field theoretical framework [10]. However, this is not
new in theoretical physics [11]. In any case, one has to
realize that there are two distinct levels of discussion in our approach.
At the spacetime level, where the actual deformations
in the string shape take place, the formulation is fully relativistic, as
witnessed by the covariant structure of our equations with
respect to the Lorentzian indices. However, at the loop space level,
where each ``point'' is representative of a particular loop
configuration, our formulation is quantum mechanical, in the sense that the
string coordinates
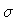 and A are not treated equally, as it is manifest, for
instance, in the loop Schrödinger equation (7). As a matter
of fact, this is the very reason for referring to that equation as the
``Schrodinger equation'' of string dynamics: the timelike
variable A enters the equation through a first order partial
derivative, as opposed to the functional ``laplacian'', which is of second
order with respect to the spacelike variables
and A are not treated equally, as it is manifest, for
instance, in the loop Schrödinger equation (7). As a matter
of fact, this is the very reason for referring to that equation as the
``Schrodinger equation'' of string dynamics: the timelike
variable A enters the equation through a first order partial
derivative, as opposed to the functional ``laplacian'', which is of second
order with respect to the spacelike variables 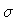 .
Far from being
an artifact of our formulation, we emphasize that this spacetime
covariant, quantum mechanics of loops, is a direct
consequence of the Hamilton-Jacobi formulation of classical string dynamics.
This is especially evident in the form of the classical
area- Hamiltonian, equation (11), from which, via the correspondence
principle, we have derived the loop Schrödinger equation.
.
Far from being
an artifact of our formulation, we emphasize that this spacetime
covariant, quantum mechanics of loops, is a direct
consequence of the Hamilton-Jacobi formulation of classical string dynamics.
This is especially evident in the form of the classical
area- Hamiltonian, equation (11), from which, via the correspondence
principle, we have derived the loop Schrödinger equation.
Incidentally, our formulation raises the interesting question as to
whether it is possible to ``covariantize'' the Schrödinger equation in
loop space, i.e., to treat the spacelike and timelike
generalized coordinates on the same footing. At the moment this is an
open problem. However, if history is any guide, one might think of
generalizing the loop Shrodinger equation into a functional
Klein-Gordon equation, or, to follow Dirac's pioneering work
and take the ``square root'' of the functional laplacian in order to
arrive at a first order functional equation for string loops.
This second route would involve an extension of Clifford's algebra along the lines
suggested, for instance, by Hosotani in the case of a membrane [4].
Be that as it may, with our present quantum mechanical formulation,
we have given a concrete meaning to the fractalization of a string
orbit's in spacetime in terms of the shape uncertainty
principle. We have concluded that the Hausdorff dimension of a quantum
string's world-surface is three, and that two distinct geometric
phases exist above and below the loop De Broglie area. We must emphasize
that
D H = 3 represents a limiting value of the Hausdorff
dimension, in the sense specified in Section 4. In actual
fact, the world-surface of
a quantum string is literally ``fuzzy'' to a degree which
depends critically on the parameter 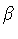 ,
the ratio between
temporal and spatial resolution. Self similarity, we have shown,
corresponds to a constant value of
,
the ratio between
temporal and spatial resolution. Self similarity, we have shown,
corresponds to a constant value of 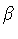 ,
with
D H = 3.
In such a case, the shape
shifting fluctuations generated by petal addition, effectively give rise
to a full transverse dimension in the string stack.
,
with
D H = 3.
In such a case, the shape
shifting fluctuations generated by petal addition, effectively give rise
to a full transverse dimension in the string stack.
As a final remark, we note that the quantum mechanical approach
discussed in this paper is in no way restricted to string-like objects.
In principle, it can be extended to any quantum p-brane, and we
anticipate that the limiting value of the corresponding fractal
dimension would be
D H = p + 2. Then, if the above over all picture is
correct, p-brane fuzziness not only acquires a well defined meaning,
but points to a fundamental change in our perception of physical
spacetime. Far from being a smooth, four-dimensional manifold
assigned ``ab initio'', spacetime is, rather, a ``process in the
making'', showing an ever changing fractal structure which responds
dynamically to the resolving power of the detecting apparatus.



Next: Bibliography
Up: Hausdorff Dimension of a
Previous: 4.2 Classical-to-fractal geometric transition
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY