


Next: 2.2 Plane wave solution
Up: 2. A functional approach
Previous: 2. A functional approach
2.1 The loop propagator and the loop Schrodinger equation
A useful starting point of our discussion is the exact form of the
string quantum kernel discussed in Ref. [3], namely
![\begin{displaymath}K [ C , C _{0} ; A ]
=
\left(
\frac{m ^{2}}{2 i \pi A}
\r...
... _{\mu \nu} (C) - \sigma _{\mu \nu} (C _{0}) \right]
\right\}
\end{displaymath}](img6.gif) |
(1) |
where m 2 is defined in terms of the string tension,
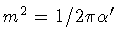 ,
,
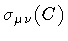 is the area element of the loop
is the area element of the loop
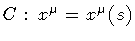 [6], i.e.
[6], i.e.
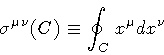 |
(2) |
and A is the proper area of the string manifold,
invariant under reparametrization of the world-sheet
coordinates
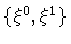
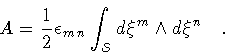 |
(3) |
The geometric doublet (
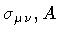 )
represents the set of
dynamical variables in our formulation of string dynamics. This
choice makes it possible to develop a Hamilton-Jacobi theory of
string loops which represents a natural extension of the familiar
formulation of classical and quantum mechanics of point-particles
[2], [3]. With hindsight, the analogy becomes
transparent when one compares Eq. (1) with the
amplitude for a relativistic particle of mass m to
propagate from
)
represents the set of
dynamical variables in our formulation of string dynamics. This
choice makes it possible to develop a Hamilton-Jacobi theory of
string loops which represents a natural extension of the familiar
formulation of classical and quantum mechanics of point-particles
[2], [3]. With hindsight, the analogy becomes
transparent when one compares Eq. (1) with the
amplitude for a relativistic particle of mass m to
propagate from
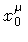 to
to 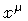 in a proper-time lapse T:
in a proper-time lapse T:
![\begin{displaymath}K ( x , x _{0} ; T)
=
\left( \frac{m}{2 \pi T} \right) ^{2}...
...\frac{i m}{2 T}
\vert x - x _{0} \vert ^{2}
\right]
\quad .
\end{displaymath}](img16.gif) |
(4) |
This comparison suggests the following correspondence between
dynamical variables for particles and strings: a particle position in
spacetime is labelled by four real numbers 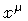 which represent
the projection of the particle position vector along the
coordinate axes. In the string case, the conventional choice is to
consider the position vector for each constituent point , and then
follow their individual dynamical evolution in terms of the
coordinate time x 0, or the proper time
which represent
the projection of the particle position vector along the
coordinate axes. In the string case, the conventional choice is to
consider the position vector for each constituent point , and then
follow their individual dynamical evolution in terms of the
coordinate time x 0, or the proper time 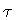 .
As a matter of fact,
the canonical string quantization is usually implemented in the
proper time gauge
.
As a matter of fact,
the canonical string quantization is usually implemented in the
proper time gauge 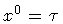 .
However, this choice explicitly breaks
the reparametrization invariance of the theory, whereas in the
Hamilton-Jacobi formulation of string dynamics, we have insisted
that reparametrization invariance be manifest at every stage.
The form (1) of the string propagator reflects that requirement.
We shall call
.
However, this choice explicitly breaks
the reparametrization invariance of the theory, whereas in the
Hamilton-Jacobi formulation of string dynamics, we have insisted
that reparametrization invariance be manifest at every stage.
The form (1) of the string propagator reflects that requirement.
We shall call
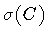 the string configuration tensor which
plays the same role as the position vector in the point-particle
case. Indeed, the six components of
the string configuration tensor which
plays the same role as the position vector in the point-particle
case. Indeed, the six components of
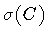 represent the projection
of the loop area onto the coordinate planes in spacetime. Likewise,
the reparametrization invariant evolution parameter for the string
turns out to be neither the coordinate time, nor the proper time of
the constituent points, but the proper area A of the whole
string manifold. As a matter of fact, the string
world-sheet is the spacetime image, through the embedding
represent the projection
of the loop area onto the coordinate planes in spacetime. Likewise,
the reparametrization invariant evolution parameter for the string
turns out to be neither the coordinate time, nor the proper time of
the constituent points, but the proper area A of the whole
string manifold. As a matter of fact, the string
world-sheet is the spacetime image, through the embedding
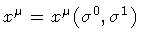 ,
of a two dimensional manifold of coordinates
,
of a two dimensional manifold of coordinates
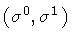 .
Thus, just as the proper time
.
Thus, just as the proper time 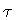 is a
measure of the timelike distance between the final and
initial position of a point particle,
the proper area A is a measure of the timelike, or
parametric distance between C and C 0, i.e., the final and the
initial configuration of the string. This idea was originally proposed
by Eguchi [5].
is a
measure of the timelike distance between the final and
initial position of a point particle,
the proper area A is a measure of the timelike, or
parametric distance between C and C 0, i.e., the final and the
initial configuration of the string. This idea was originally proposed
by Eguchi [5].
It may seem less clear which interior area must be assigned to
any given loop, as one can imagine infinite different surfaces having
the loop as a unique boundary. However, once we
accept the idea to look at the area of a surface S C
as a sort of time label for its boundary
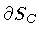 ,
then the
arbitrariness in the assignment of S C corresponds to the
usual freedom to reset the initial instant of time
for our clock. The important point is that, once the initial area
has been chosen, the string clock measures area lapses.
In summary, then,
,
then the
arbitrariness in the assignment of S C corresponds to the
usual freedom to reset the initial instant of time
for our clock. The important point is that, once the initial area
has been chosen, the string clock measures area lapses.
In summary, then,
![$\left[ \sigma ^{\mu \nu} (C) - \sigma ^{\mu \nu} (C _{0}) \right] ^{2}$](img23.gif) represents the ``spatial distance squared'' between C and
C 0, and A represents the classical time lapse for the string to
change its shape from C 0 to C.
represents the ``spatial distance squared'' between C and
C 0, and A represents the classical time lapse for the string to
change its shape from C 0 to C.
The quantum formulation of string-dynamics based on these
non-canonical variables was undertaken in [3] with
the evaluation of the string
kernel and the derivation of the Schrödinger loop equation.
Presently, we are interested in the quantum fluctuations of a loop. By
this, we mean a shape-changing transition, and we would like to
assign a probability amplitude to any such process. In order to do
this, we make use of ``areal, or loop, derivatives'', as
developed, for instance, by Migdal [6]. It may be useful to review
briefly how loop derivatives work, since they
are often confused with ordinary functional derivatives in view
of the formal relation
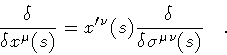 |
(5) |
However, there is a basic difference between these two types of operation.
To begin with, an infinitesimal shape variation corresponds to
``cutting'' the loop C at a particular point, say y, and then
joining the two end-points to an infinitesimal loop
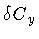 .
Accordingly,
.
Accordingly,
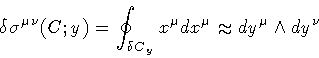 |
(6) |
where
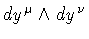 is the elementary oriented
area subtended by
is the elementary oriented
area subtended by
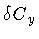 .
A suggestive description of
this procedure, due to Migdal [6],
is that of adding a ``petal'' to the original loop. Then, we can speak of an
``intrinsic distance'' between the deformed and initial strings, as the
infinitesimal, oriented area variation,
.
A suggestive description of
this procedure, due to Migdal [6],
is that of adding a ``petal'' to the original loop. Then, we can speak of an
``intrinsic distance'' between the deformed and initial strings, as the
infinitesimal, oriented area variation,
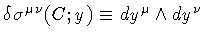 .
``Intrinsic'', here, means that the
(spacelike) distance is invariant under reparametrization
and/or embedding transformations. Evidently, there is no
counterpart of this operation in the case of point-particles, because of
the lack of spatial extension. Note that, while
.
``Intrinsic'', here, means that the
(spacelike) distance is invariant under reparametrization
and/or embedding transformations. Evidently, there is no
counterpart of this operation in the case of point-particles, because of
the lack of spatial extension. Note that, while
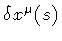 represents a smooth deformation of the loop
represents a smooth deformation of the loop
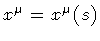 ,
the addition
of a petal introduces a singular ``cusp'' at the contact
point. Moreover, cusps produce
infinities in the ordinary variational derivatives but
not in the area derivatives [6].
,
the addition
of a petal introduces a singular ``cusp'' at the contact
point. Moreover, cusps produce
infinities in the ordinary variational derivatives but
not in the area derivatives [6].
Non-differentiability is the hallmark of fractal objects.
Thus, anticipating one of our results, quantum loop fluctuations,
interpreted as singular shape-changing transitions resulting
from
``petal addition'', are responsible for the fractalization of the string.
Evidently, in order to give substance to this idea, we must formulate
the shape uncertainty principle for loops, and the centerpiece of this
whole discussion becomes the loop wave functional
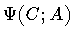 ,
whose precise meaning we now wish to discuss.
,
whose precise meaning we now wish to discuss.
Suppose the shape of the initial string is approximated by
the loop configuration
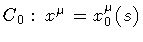 .
The corresponding ``wave packet''
.
The corresponding ``wave packet''
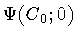 will be concentrated around C 0. As the areal
time increases, the initial string evolves, sweeping a world-sheet of
parametric proper area A.
Once
will be concentrated around C 0. As the areal
time increases, the initial string evolves, sweeping a world-sheet of
parametric proper area A.
Once
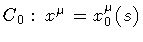 and A are assigned,
the final string
and A are assigned,
the final string
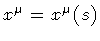 can attain any of the
different shapes compatible with the given initial condition and with
the extension of the world-sheet. Each geometric configuration
corresponds to a different ``point'' in loop space [3]. Then,
can attain any of the
different shapes compatible with the given initial condition and with
the extension of the world-sheet. Each geometric configuration
corresponds to a different ``point'' in loop space [3]. Then,
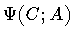 will represent the probability amplitude to find a string of shape
will represent the probability amplitude to find a string of shape
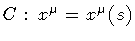 as the final boundary of the
world-surface, of proper area A, originating from C 0.
From this vantage point, the quantum string evolution is a random
shape-shifting
process which corresponds, mathematically, to the spreading
of the initial wave packet
as the final boundary of the
world-surface, of proper area A, originating from C 0.
From this vantage point, the quantum string evolution is a random
shape-shifting
process which corresponds, mathematically, to the spreading
of the initial wave packet
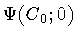 throughout loop space.
The wavefunctional
throughout loop space.
The wavefunctional
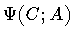 can be obtained either by solving the
loop Schrödinger equation
can be obtained either by solving the
loop Schrödinger equation
![\begin{displaymath}-
\frac{1}{4 m ^{2}}
\left( \oint _{C} dl (s) \right) ^{-1}...
... (s)}
=
i
\frac{\partial \Psi [C ; A]}{\partial A}
\quad ,
\end{displaymath}](img34.gif) |
(7) |
where,
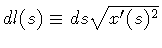 is the
invariant element of string length,
or by means of the amplitude (1), summing over all the initial
string configurations. This amounts to integrate over all the allowed loop
configurations
is the
invariant element of string length,
or by means of the amplitude (1), summing over all the initial
string configurations. This amounts to integrate over all the allowed loop
configurations
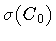 :
:
Equation (7), we recall, is the quantum transcription,
through the Correspondence Principle,
of the classical relation between the area-hamiltonian H
and the loop momentum density
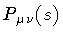 [3]:
[3]:
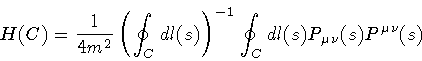 |
(11) |
Once again, we note the analogy between Eq.(11) and the
familiar energy momentum relation for a point particle,
H = p 2 / 2 m.
We shall comment on the ``non-relativistic'' form of Eq. (11) in
the concluding section of this paper. Presently, we limit ourselves to
note that the difference between the point-particle case and the
string case, stems from the spatial extension of the loop,and is
reflected in Eq. (11) by the averaging integral of the
momentum squared along the loop itself. Equation
(11) represents the total loop energy instead of the energy
of a single constituent string bit. Just
as the particle linear momentum gives the direction along
which a particle moves and the rate of position change, so the
loop momentum describes the deformation in the loopshape and
the rate of shape change. The corresponding hamiltonian describes
the energy variation as the loop area varies, irrespective of the
actual point along the loop where the deformation takes place.
Accordingly, the hamiltonian (9) represents the
generating operator of the loop area variations, and
the momentum density (10) represents the generator of the
deformations in the loop shape at the point
 .
.
From the above discussion, we are led to conclude that:
- 1.
- deformations may occur randomly at any point on the
loop;
- 2.
- the antisymmetry in the indices
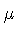 ,
,
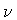 guarantees that
guarantees that
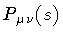 generates orthogonal
deformations only, i.e.
generates orthogonal
deformations only, i.e.
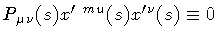 ;
;
- 3.
- shape changes cost energy because of the string
tension and the fact that, adding a small loop, or ``petal'', increases
the total length of the string;
- 4.
- the energy balance condition is provided by equation
(11) at the classical level and by equation (7)
at the quantum level. In both cases the global energy variation
per unit proper area is obtained by a loop average of the
double deformation at single point.
1), 2), 3), 4)
represent the distinctive features of the
string quantum shape shifting phenomenon.



Next: 2.2 Plane wave solution
Up: 2. A functional approach
Previous: 2. A functional approach
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![\begin{displaymath}K [ C , C _{0} ; A ]
=
\left(
\frac{m ^{2}}{2 i \pi A}
\r...
... _{\mu \nu} (C) - \sigma _{\mu \nu} (C _{0}) \right]
\right\}
\end{displaymath}](img6.gif)
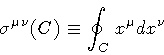
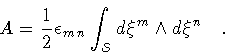
![]() )
represents the set of
dynamical variables in our formulation of string dynamics. This
choice makes it possible to develop a Hamilton-Jacobi theory of
string loops which represents a natural extension of the familiar
formulation of classical and quantum mechanics of point-particles
[2], [3]. With hindsight, the analogy becomes
transparent when one compares Eq. (1) with the
amplitude for a relativistic particle of mass m to
propagate from
)
represents the set of
dynamical variables in our formulation of string dynamics. This
choice makes it possible to develop a Hamilton-Jacobi theory of
string loops which represents a natural extension of the familiar
formulation of classical and quantum mechanics of point-particles
[2], [3]. With hindsight, the analogy becomes
transparent when one compares Eq. (1) with the
amplitude for a relativistic particle of mass m to
propagate from
![]() to
to ![]() in a proper-time lapse T:
in a proper-time lapse T:
![\begin{displaymath}K ( x , x _{0} ; T)
=
\left( \frac{m}{2 \pi T} \right) ^{2}...
...\frac{i m}{2 T}
\vert x - x _{0} \vert ^{2}
\right]
\quad .
\end{displaymath}](img16.gif)
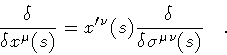
![]() .
.