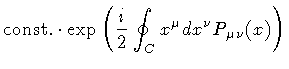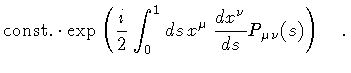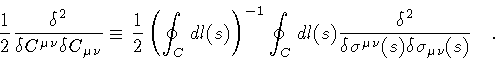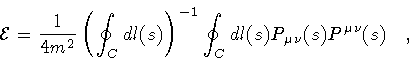Next: 2.3 Gaussian Loop-wavepacket
Up: 2. A functional approach
Previous: 2.1 The loop propagator
2.2 Plane wave solution
The next step in our program to set up a (spacetime covariant) functional
quantum mechanics of closed strings, is to find the basic
solutions of equation (7). As in the quantum mechanics of
point particles, we seek first plane-wave solutions
The overall constant in the above equation will be fixed by a
suitable normalization condition.
Apart from that, the wave functional (12) represents an
eigenstate of the loop total momentum operator
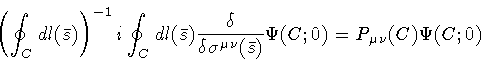 |
(13) |
with eigenvalues
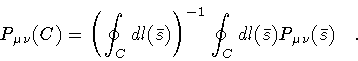 |
(14) |
Note that, while
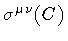 is a
functional of the loop C, i.e., it contains no reference to a
special point of the loop,
the area derivative
is a
functional of the loop C, i.e., it contains no reference to a
special point of the loop,
the area derivative
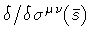 operates at the contact point
operates at the contact point
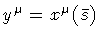 .
Thus,
the area derivative of a functional is no longer a functional. Even if the
functional under derivation is reparametrization invariant, its
area derivative behaves as a scalar density under redefinition
of the loop coordinate. In order to recover reparametrization
invariance, we have to get rid of the arbitrariness in the choice of the
attachment point. This can be achieved by summing over all its possible
locations along the loop, and then compensating for the
overcounting of the area variation by averaging the result over the proper
length of the loop. This is what we have done in equations
(13) and (14), thereby trading
the string momentum density
.
Thus,
the area derivative of a functional is no longer a functional. Even if the
functional under derivation is reparametrization invariant, its
area derivative behaves as a scalar density under redefinition
of the loop coordinate. In order to recover reparametrization
invariance, we have to get rid of the arbitrariness in the choice of the
attachment point. This can be achieved by summing over all its possible
locations along the loop, and then compensating for the
overcounting of the area variation by averaging the result over the proper
length of the loop. This is what we have done in equations
(13) and (14), thereby trading
the string momentum density
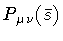 ,
i.e. a
function of the loop coordinate
,
i.e. a
function of the loop coordinate 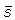 ,
with a
functional loop momentum
,
with a
functional loop momentum
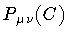 .
The same
prescription enables us to define any other reparametrization
invariant derivative operator.
Hence, we introduce a simpler but more effective
notation, and define the loop derivative as
.
The same
prescription enables us to define any other reparametrization
invariant derivative operator.
Hence, we introduce a simpler but more effective
notation, and define the loop derivative as
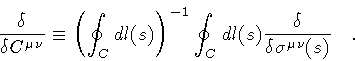 |
(15) |
This represents a genuine loop operation withoutn reference to
the way in which the loop is parametrized.
With the above remarks in mind, the functional Laplacian
operator appearing in equation (7) is
reparametrization and Lorentz invariant,
and is constructed according to the same prescription: attach two
petals at the loop point s, then compute the functional variation
and, finally, average over all possible locations of the attachment
point. In the notation (15), the loop laplacian
reads
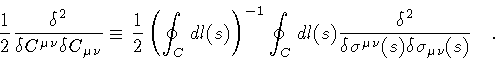 |
(16) |
Then, if we factorize the explicit A-dependence of the wave functional
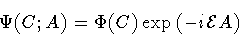 |
(17) |
the stationary functional wave equation takes the form
![\begin{displaymath}-
\frac{1}{4 m ^{2}}
\frac{\delta ^{2} \Psi [C ; A]}
{\del...
...elta C _{\mu \nu}}
=
{\mathcal{E}}
\,
\Psi[C ; A]
\quad .
\end{displaymath}](img64.gif) |
(18) |
Thus, we need to evaluate the second functional variation of
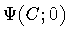 corresponding to the addition of two petals to C, say at the point
corresponding to the addition of two petals to C, say at the point
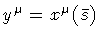 .
The first variation of
.
The first variation of
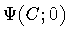 can be obtained from Eq. (12)
can be obtained from Eq. (12)
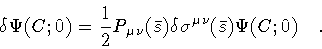 |
(19) |
Reopening the loop C at the same contact point and adding a second
infinitesimal loop, we arrive at the second variation of
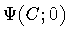 ,
,
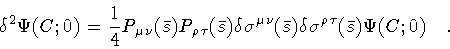 |
(20) |
Then, Eq. (12) solves equation (7) if
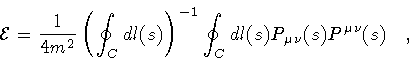 |
(21) |
which is the classical dispersion relation between string energy
and momentum. Having determined a set of solutions to
the stationary part of equation (7), the
complete solutions describing the quantum evolution from an
initial state
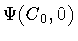 to a final state
to a final state
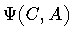 can
be obtained by means of the amplitude (1), as follows
can
be obtained by means of the amplitude (1), as follows
As one would expect, the solution (22) represents a
``monocromatic string wave train'' extending all over loop space.



Next: 2.3 Gaussian Loop-wavepacket
Up: 2. A functional approach
Previous: 2.1 The loop propagator
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY