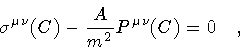Next: 3. The Shape Uncertainty
Up: 2. A functional approach
Previous: 2.2 Plane wave solution
2.3 Gaussian Loop-wavepacket
The quantum state represented by Eq.(12) is completely de-localized
in loop space, which means that all the string shapes
are equally probable, or that the string has no definite shape at all.
Even though the wave functional (22) is a
solution of equation (7), it does not have an immediate
physical interpretation: at most, it can be used to describe a
flux in loop space rather than to describe a single physical
object. Physically acceptable one-string states are obtained by a suitable
superposition of ``elementary'' plane wave solutions. The quantum
state closest to a classical string will be described by a
Gaussian wave packet,
| |
|
![$\displaystyle \Psi [C _{0} ; 0]
=
\left[ \frac{1}{2 \pi ( \Delta \sigma ) ^{2}}...
...eft(
\frac{i}{2}
\oint _{C _{0}} x ^{\mu} d x ^{\nu} P _{\mu \nu}
\right)
\cdot$](img75.gif) |
|
| |
|
![$\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \cdot
\exp
\left...
...ma) ^{2}}
\left(
\oint _{C _{0}} x^{\mu} dx ^{\nu}
\right) ^{2}
\right]
\quad ,$](img76.gif) |
(23) |
where
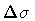 represents the width, or position
uncertainty in loop space, corresponding to an uncertainty in the
physical shape of the loop. By inserting Eq. (23) into
Eq. (8), and integrating out
represents the width, or position
uncertainty in loop space, corresponding to an uncertainty in the
physical shape of the loop. By inserting Eq. (23) into
Eq. (8), and integrating out
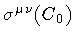 ,
we find
,
we find
The wave functional represented by equation
(24) spreads throughout loop space in conformity with the laws of
quantum mechanics. In particular, the center of the wave
packet moves according to the stationary phase principle, i.e.
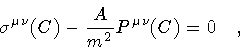 |
(25) |
and the width broadens as A increases
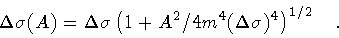 |
(26) |
Thus, as discussed previously, A represents a measure
of the ``time-like'' distance between the initial and final string loop.
Then,
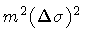 represent the wavepacket mean
life. As long as
represent the wavepacket mean
life. As long as
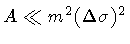 ,
the wavepacket
maintains its original width
,
the wavepacket
maintains its original width
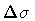 .
However, as A
increases with respect to
.
However, as A
increases with respect to
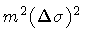 ,
the
wavepacket becomes broader and the initial string
shape decays in the background space.
Notice that, for sharp initial wave packets, i.e., for
,
the
wavepacket becomes broader and the initial string
shape decays in the background space.
Notice that, for sharp initial wave packets, i.e., for
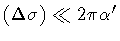 ,
the shape shifting
process is more ``rapid'' than for large wave packets.
Hence, strings with a well defined initial shape will sink
faster into the sea of quantum fluctuations than broadly
defined string loops.
,
the shape shifting
process is more ``rapid'' than for large wave packets.
Hence, strings with a well defined initial shape will sink
faster into the sea of quantum fluctuations than broadly
defined string loops.



Next: 3. The Shape Uncertainty
Up: 2. A functional approach
Previous: 2.2 Plane wave solution
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![$\displaystyle \Psi [C _{0} ; 0]
=
\left[ \frac{1}{2 \pi ( \Delta \sigma ) ^{2}}...
...eft(
\frac{i}{2}
\oint _{C _{0}} x ^{\mu} d x ^{\nu} P _{\mu \nu}
\right)
\cdot$](img75.gif)
![$\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \cdot
\exp
\left...
...ma) ^{2}}
\left(
\oint _{C _{0}} x^{\mu} dx ^{\nu}
\right) ^{2}
\right]
\quad ,$](img76.gif)