


Next: 4. Fractal Strings
Up: Hausdorff Dimension of a
Previous: 2.3 Gaussian Loop-wavepacket
3. The Shape Uncertainty Principle
In this section we discuss the new form that the uncertainty principle
takes in the functional theory of string loops.
Let us consider a Gaussian momentum wave function
![\begin{displaymath}\Phi (P)
=
\frac{1}{\left[ \pi (\Delta P) ^{2} \right] ^{3/...
...)
\left(P _{\mu \nu} (s) - K _{\mu \nu} \right) ^{2}
\right]
\end{displaymath}](img87.gif) |
(27) |
where
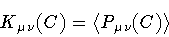 |
(28) |
represents the string momentum mean value around which the
Gaussian wavepacket is centered, and
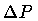 is a measure of the momentum dispersion in the wavepacket.
is a measure of the momentum dispersion in the wavepacket.
Thus,
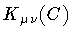 is a reparametrization invariant
functional of the loop C representing the string
``drift'' through loop space.
is a reparametrization invariant
functional of the loop C representing the string
``drift'' through loop space.
In order to arrive at the shape uncertainty principle, we first
evaluate the quantum average of the loop squared momentum
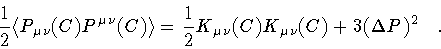 |
(29) |
Therefore, the string momentum mean square deviation, or
uncertainty squared, is
The wave functional in configuration space is obtained by
Fourier transforming Eq. (27):
This is again a Gaussian wavepacket, whose ``center of mass''
moves in loop space with a momentum
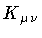 .
Accordingly, the loop probability density still has a Gaussian form
.
Accordingly, the loop probability density still has a Gaussian form
centered around the vanishing loop with a dispersion given by
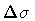 .
By means of the density (32), we obtain
.
By means of the density (32), we obtain
Then, comparing Eq. (34) with Eq. (30), we find
that the uncertainties are related by
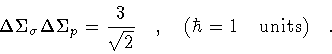 |
(35) |
Equation (35) represents the new form that the Heisenberg
principle takes when string quantum mechanics is formulated in terms
of diffusion in loop space, or quantum shape shifting. Just as a
pointlike particle cannot have a definite position in space
and a definite linear momentum at the same time, a physical
string cannot have a definite shape and a
definite rate of shape changing at a given areal time.
In other words, a string loop cannot be totally at rest neither in
physical nor in loop space: it is subject to a zero-point motion
characterized by
In such a state a physical string undergoes a zero-point
shape shifting, and the loop momentum attains its minimum
value compatible with an area resolution
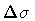 .
.
To keep ourselves as close as possible to Heisenberg's seminal
idea, we interpret the lack of a definite shape
as follows: as we increase the resolution of the ``microscope''
used to probe the structure of the string, more and more quantum petals
will appear along the loop. The picture emerging out of this is
that of a classical line turning into a fractal object as
we move from the classical domain of physics to the quantum
realm of quantum fluctuations. If so, two questions immediately
arise:
- 1.
- a classical bosonic string is a closed line of
topological dimension one. Its spacetime image consists of a
smooth, timelike, two-dimensional world-sheet. Then, if a quantum
string is a fractal object, which Hausdorff dimension
should be assigned to it?
- 2.
- Is there any critical scale characterizing the
classical-to-fractal geometrical transition?
These two questions will be addressed in the next section.



Next: 4. Fractal Strings
Up: Hausdorff Dimension of a
Previous: 2.3 Gaussian Loop-wavepacket
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![\begin{displaymath}\Phi (P)
=
\frac{1}{\left[ \pi (\Delta P) ^{2} \right] ^{3/...
...)
\left(P _{\mu \nu} (s) - K _{\mu \nu} \right) ^{2}
\right]
\end{displaymath}](img87.gif)
![$\displaystyle \left[
\frac{1}{2}
\langle P _{\mu \nu} (C) P ^{\mu \nu} (C) \rangle
\right] ^{1/2}$](img109.gif)