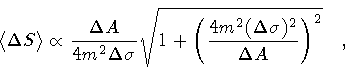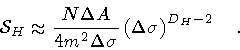Next: 4.2 Classical-to-fractal geometric transition
Up: 4. Fractal Strings
Previous: 4. Fractal Strings
4.1 The Hausdorf dimension of a quantum string
One of the major achievements of Feynman's formulation of quantum
mechanics was to restore the particle's trajectory
concept at the quantum level.
However, the dominant contribution to the ``sum over histories''
is provided by trajectories which are nowhere differentiable
[7]. Non differentiability is the hallmark of fractal lines.
In fact, it seems that Feynman and Hibbs were aware that the
quantum mechanical path of a particle is inherently fractal.
This idea was revisited, and further explored by Abbott and
Wise in the case of a free non-relativistic particle [8],
and the extension to relativistic particles was carried out by
several authors, but without a general agreement [9].
This is one of the reasons for setting up a quantum mechanical,
rather than a field theoretical, framework, even for relativistic
objects. It enables us to adapt the Abbott-Wise discussion to
the string case, with the following basic substitution:
the point particle, erratically moving through euclidean space,
is replaced by the string configuration whose representative
point randomly drifts through loop space. We have shown in the
previous sections that ``flow of time'' for particles is
replaced by area variations for strings. Hence, the image of
an abstract linear ``trajectory'' connecting the two ``points'' C 0
and C in a lapse of time A, corresponds, physically, to
a family of closed lines stacked into a two-dimensional surface
of proper area A. Here is where the quantum mechanical aspect of our
approach, and our choice of dynamical variables, seem to have
a distinct advantage over the more conventional
relativistic description of string dynamics. The conventional
picture of a string world-surface, consisting of a collection of
world-lines associated with each constituent point, is replaced by a
world-sheet ``foliation'' consisting of a stack of closed lines labelled
by the internal parameter A. In other words, we interpret
the string world-surface as a sequence of ``snapshots'' of single
closed lines ordered with respect to the interior area bounded by
them. Then, the randomness of the ``motion'' of a point in loop space
is a reflection of the non-differentiability of the string
world-sheet, which, in turn, is due to zero-point quantum
fluctuations: the random addition of petals to each loop results in a
fuzziness, or graininess of the world surface, by which the string stack
acquires an effective thickness. One can expect that this
graininess becomes apparent only when one can resolve the
surface small irregularities.
The technical discussion on which this picture is based, follows
closely the analysis by Abbott and Wise [8]. Thus, let us
divide the string internal coordinates domain into
N strips of area 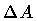 .
Accordingly, the string stack is
approximated by the discrete set of the N + 1 loops,
.
Accordingly, the string stack is
approximated by the discrete set of the N + 1 loops,
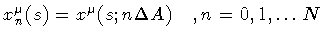 .
Suppose now that we take a snapshot of each one of them, and measure their
internal area. If the cross section of the emulsion grains is
.
Suppose now that we take a snapshot of each one of them, and measure their
internal area. If the cross section of the emulsion grains is
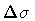 ,
then we have an area indeterminacy
,
then we have an area indeterminacy
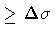 .
Then, the total area of the surface subtended by the last and
first loop in the stack will be given by
.
Then, the total area of the surface subtended by the last and
first loop in the stack will be given by
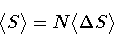 |
(38) |
where
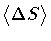 is the average area
variation in the interval
is the average area
variation in the interval 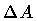 ,
,
![\begin{displaymath}\langle \Delta S \rangle
\equiv
\left[
\int [{\mathcal{D}}...
... \vert \Psi (C ; \Delta A) \vert ^{2}
\right] ^{1/2}
\quad .
\end{displaymath}](img116.gif) |
(39) |
The finite resolution in 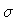 is properly taken into
account by choosing a gaussian wave
functional of the type (23) for
is properly taken into
account by choosing a gaussian wave
functional of the type (23) for
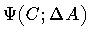 .
Next, following our correspondence code between particles
and strings, we define the Hausdorff measure
.
Next, following our correspondence code between particles
and strings, we define the Hausdorff measure
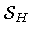 for
the stack of fluctuating loops through the relation
for
the stack of fluctuating loops through the relation
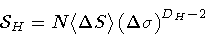 |
(40) |
where D H is a number determined by the requirement that
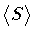 be independent of
the resolution
be independent of
the resolution
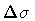 .
.
In the above calculation, we may represent the
quantum state of the string by the loop functional
![\begin{displaymath}\Psi(C)
=
\int \frac{[{\mathcal{D}} P _{\mu \nu} (s)]}{(2 \...
...
\exp \frac{i}{2} \oint _{C} P _{\mu \nu} x ^{\mu} d x ^{\nu}
\end{displaymath}](img122.gif) |
(41) |
with a gaussian momentum distribution 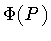 centered
around a vanishing string average momentum
centered
around a vanishing string average momentum
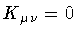 ,
i.e., for the moment, we consider a free loop
subject only to zero-point fluctuations.
Then,
,
i.e., for the moment, we consider a free loop
subject only to zero-point fluctuations.
Then,
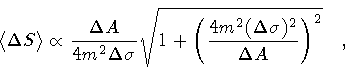 |
(42) |
and, in order to determine the string fractal dimension we keep
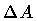 fixed and take the limit
fixed and take the limit
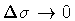 :
:
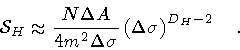 |
(43) |
Hence, in order to eliminate the dependence on
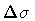 ,
,
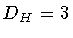 .
As in the point particle case, quantum
fluctuations increase by one unit the dimension of the
string classical path. As discussed in the following subsection,
the gradual appearance of an extra dimension is perceived as
fuzziness of the string manifold, and the next question to be
addressed is which parameter, in our quantum mechanical approach,
controls the transition from classical to fractal geometry.
.
As in the point particle case, quantum
fluctuations increase by one unit the dimension of the
string classical path. As discussed in the following subsection,
the gradual appearance of an extra dimension is perceived as
fuzziness of the string manifold, and the next question to be
addressed is which parameter, in our quantum mechanical approach,
controls the transition from classical to fractal geometry.



Next: 4.2 Classical-to-fractal geometric transition
Up: 4. Fractal Strings
Previous: 4. Fractal Strings
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() .
Accordingly, the string stack is
approximated by the discrete set of the N + 1 loops,
.
Accordingly, the string stack is
approximated by the discrete set of the N + 1 loops,
![]() .
Suppose now that we take a snapshot of each one of them, and measure their
internal area. If the cross section of the emulsion grains is
.
Suppose now that we take a snapshot of each one of them, and measure their
internal area. If the cross section of the emulsion grains is
![]() ,
then we have an area indeterminacy
,
then we have an area indeterminacy
![]() .
Then, the total area of the surface subtended by the last and
first loop in the stack will be given by
.
Then, the total area of the surface subtended by the last and
first loop in the stack will be given by
![\begin{displaymath}\langle \Delta S \rangle
\equiv
\left[
\int [{\mathcal{D}}...
... \vert \Psi (C ; \Delta A) \vert ^{2}
\right] ^{1/2}
\quad .
\end{displaymath}](img116.gif)
![\begin{displaymath}\Psi(C)
=
\int \frac{[{\mathcal{D}} P _{\mu \nu} (s)]}{(2 \...
...
\exp \frac{i}{2} \oint _{C} P _{\mu \nu} x ^{\mu} d x ^{\nu}
\end{displaymath}](img122.gif)