

Next: 3 Path integral quantization
Up: 2 General analysis of
Previous: 2.1 Path integral
2.2 The signature of the mass generation:
ordinary versus tachyonic
In this subsection we turn to the analysis of the contribution
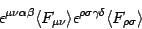 |
(13) |
of equation (12), which will be responsible
for ordinary or tachyonic mass generation according to whether
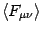 represents an external magnetic or
electric field. We notice that our results are not inconsistent with
those that can be deduced from [8, equation (31)],
from which it is clear that the sign of the contribution from the
interaction lagrangian changes in the case of purely electric or
purely magnetic background.
represents an external magnetic or
electric field. We notice that our results are not inconsistent with
those that can be deduced from [8, equation (31)],
from which it is clear that the sign of the contribution from the
interaction lagrangian changes in the case of purely electric or
purely magnetic background.
Let us now start from the case of a constant magnetic field 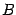 . Then,
without loosing generality, we can rotate the reference frame to align
an axis, say
. Then,
without loosing generality, we can rotate the reference frame to align
an axis, say 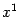 , with
, with 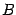 . Accordingly,
. Accordingly,
![$\langle F _{\mu \nu}
\rangle = B \delta _{[ \mu \vert 2} \delta _{ \nu ] 3}$](img49.gif) , so that
, so that
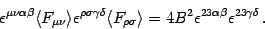 |
(14) |
It is clear thus that 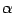 ,
, 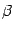 ,
, 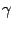 and
and 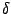 in (14) can take only the values
in (14) can take only the values 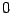 ,
, 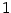 . Denoting by
. Denoting by
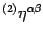 the
the 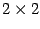 Minkowski tensor, we
must then have that
Minkowski tensor, we
must then have that
where
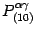 is the projector onto the
is the projector onto the
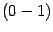 -plane, i.e.
-plane, i.e.
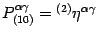 . Contracting in relation (15)
the couples of indices
. Contracting in relation (15)
the couples of indices
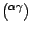 and
and
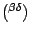 we obtain
we obtain
since in lowering the indices 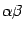 there is the time
involved,
there is the time
involved,
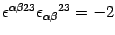 , so that
, so that 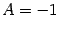 .
.
Analogously in the electric case we can take
![$F _{\mu \nu} = E \delta
_{[\mu \vert 0} \delta _{1 \vert \nu]}$](img71.gif) . Then
. Then
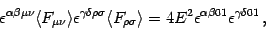 |
(16) |
with the indices 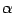 ,
, 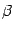 ,
, 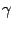 ,
, 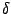 taking only the
spatial values
taking only the
spatial values 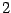 ,
, 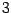 . Now, following the same procedure and
observing that no minus signs are involved in lowering spatial
indices, we find
. Now, following the same procedure and
observing that no minus signs are involved in lowering spatial
indices, we find
again we introduced the projector notation
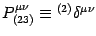 , where
, where
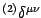 is the
is the 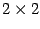 Kronecker delta.
Kronecker delta.
We can now write the equation of motion for the fluctuations, which
from the action (12) turns out to be
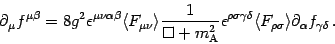 |
(17) |
The above equation can then be expressed, for both the electric and
magnetic case, in Fourier space and in terms of the vector potential
of the fluctuations, which we will call 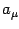 . Since
. Since
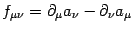 , we have
, we have
 |
(18) |
Here and in what follows we define
and
in the magnetic case, or
in the electric case. Equation (18) can be
written also as
where we have defined
 |
(21) |
The operator in (21) can be diagonalized5 as shown in appendix A. Four
linearly independent physical states satisfy the eigenvector equation
of
 ; we will call them
; we will call them  ,
,
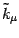 ,
,
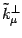 ,
, 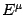 .
Their definitions and corresponding eigenvalues are enlisted in
table 1.
.
Their definitions and corresponding eigenvalues are enlisted in
table 1.
Table 1:
Eigenvalues and eigenvectors of the propagator.
|
|
There are, thus, two non-zero eigenvalues and one of them, 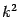 ,
has degeneracy two; moreover the ``gauge'' eigenvector is associated
to the zero eigenvalue. This last results changes if we study the
problem in the covariant
,
has degeneracy two; moreover the ``gauge'' eigenvector is associated
to the zero eigenvalue. This last results changes if we study the
problem in the covariant 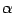 -gauge, when the
eigenvector
-gauge, when the
eigenvector 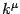 is then associated to a non-zero (but still
background independent) eigenvalue,
is then associated to a non-zero (but still
background independent) eigenvalue, 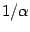 (the corresponding
inverse propagator will be called
(the corresponding
inverse propagator will be called
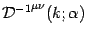 as defined in what follows).
as defined in what follows).
As promised above, we can now compare the obtained results with those
derived in previous works on the subject. Again, we observe that a key
point in our derivation is the (non-perturbative) path-integral
procedure used to obtain equation (9): in this way all
the effects due to the quantum fluctuations of the pseudoscalar field,
at all orders, are taken into account. In particular, if we
concentrate on the purely magnetic case, it is then clear that this
constitutes a generalization of the results obtained
in [5], where the secular equation is obtained
considering plane wave solutions to the classical equations of
motion associated to the Maxwell 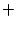 Klein-Gordon action for the
coupled electromagnetic and pseudoscalar fields. An analogous result
for the electric case in presence of massless pseudoscalars can, for
instance, be found in [17]: here the dispersion relations
are obtained under physically very sensible restrictions but are,
anyway, of perturbative character. Also the more detailed analysis
of [18] uses a different kind of approximation with
respect to the one employed in our calculation since the starting
lagrangian in [18, equation (1)] is different
from (12), our quadratic approximation to the
full, non-perturbative, effective result in
equation (9). We can thus trace back the differences
between our results for the eigenvalues of the propagator and the one
already derived in the literature on the subject, to the fact that we
have taken into account the effects due to the pseduscalar fields in a
substantially non-perturbative way.
Klein-Gordon action for the
coupled electromagnetic and pseudoscalar fields. An analogous result
for the electric case in presence of massless pseudoscalars can, for
instance, be found in [17]: here the dispersion relations
are obtained under physically very sensible restrictions but are,
anyway, of perturbative character. Also the more detailed analysis
of [18] uses a different kind of approximation with
respect to the one employed in our calculation since the starting
lagrangian in [18, equation (1)] is different
from (12), our quadratic approximation to the
full, non-perturbative, effective result in
equation (9). We can thus trace back the differences
between our results for the eigenvalues of the propagator and the one
already derived in the literature on the subject, to the fact that we
have taken into account the effects due to the pseduscalar fields in a
substantially non-perturbative way.


Next: 3 Path integral quantization
Up: 2 General analysis of
Previous: 2.1 Path integral
Stefano Ansoldi
![]() . Then,
without loosing generality, we can rotate the reference frame to align
an axis, say
. Then,
without loosing generality, we can rotate the reference frame to align
an axis, say ![]() , with
, with ![]() . Accordingly,
. Accordingly,
![]() , so that
, so that
![]() . Then
. Then
![]() Klein-Gordon action for the
coupled electromagnetic and pseudoscalar fields. An analogous result
for the electric case in presence of massless pseudoscalars can, for
instance, be found in [17]: here the dispersion relations
are obtained under physically very sensible restrictions but are,
anyway, of perturbative character. Also the more detailed analysis
of [18] uses a different kind of approximation with
respect to the one employed in our calculation since the starting
lagrangian in [18, equation (1)] is different
from (12), our quadratic approximation to the
full, non-perturbative, effective result in
equation (9). We can thus trace back the differences
between our results for the eigenvalues of the propagator and the one
already derived in the literature on the subject, to the fact that we
have taken into account the effects due to the pseduscalar fields in a
substantially non-perturbative way.
Klein-Gordon action for the
coupled electromagnetic and pseudoscalar fields. An analogous result
for the electric case in presence of massless pseudoscalars can, for
instance, be found in [17]: here the dispersion relations
are obtained under physically very sensible restrictions but are,
anyway, of perturbative character. Also the more detailed analysis
of [18] uses a different kind of approximation with
respect to the one employed in our calculation since the starting
lagrangian in [18, equation (1)] is different
from (12), our quadratic approximation to the
full, non-perturbative, effective result in
equation (9). We can thus trace back the differences
between our results for the eigenvalues of the propagator and the one
already derived in the literature on the subject, to the fact that we
have taken into account the effects due to the pseduscalar fields in a
substantially non-perturbative way.