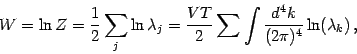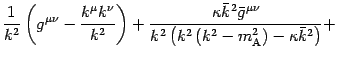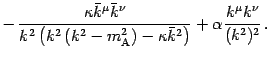

Next: 4 Evaluation of the
Up: RealImaginaryMass
Previous: 2.2 The signature of
3 Path integral quantization of small perturbations:
propagator and vacuum energy
To compute the vacuum energy we proceed further in the covariantly
quantized fashion we started in the previous section. In a covariant
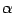 -gauge the path integral for the partition function can be
rewritten, using (21) and going to euclidean space, as
-gauge the path integral for the partition function can be
rewritten, using (21) and going to euclidean space, as
Here we have already performed the functional integration over 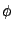 ,
we remember that we are approximating the higher order lagrangian up
to the second order in the fluctuations and understand the
path-integrals in the euclidean sector. The functional integration
over
,
we remember that we are approximating the higher order lagrangian up
to the second order in the fluctuations and understand the
path-integrals in the euclidean sector. The functional integration
over 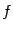 can now be done and we get
can now be done and we get
![\begin{displaymath}
Z = \frac{ \det \left[ \partial ^{2} \right] \int [ {\mathca...
...left( \Box + m _{\mathrm{A}} ^{2} \right) \right]
^{1/2} }\,,
\end{displaymath}](img113.gif) |
(23) |
where
In order to solve (23) we have to find the
eigenvalues, 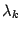 , of
, of
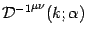 :
: 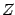 equals then the product of these eigenvalues. The
requested eigenvalues are those related to the physical polarizations
found in section 2.2, i.e.
equals then the product of these eigenvalues. The
requested eigenvalues are those related to the physical polarizations
found in section 2.2, i.e.
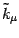 ,
,
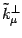 ,
, 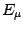 , with eigenvalues
, with eigenvalues
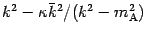 ,
, 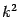 and
and
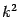 respectively. As already discussed at the end of the
previous section, the eigenvector
respectively. As already discussed at the end of the
previous section, the eigenvector 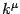 has now a non-zero
eigenvalue
has now a non-zero
eigenvalue 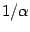 .
.
The vacuum energy, or free energy, is then
so that
The propagator, i.e. the inverse of
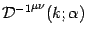 , can also be found exactly, as shown in appendix
B, and results to be
, can also be found exactly, as shown in appendix
B, and results to be

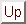

Next: 4 Evaluation of the
Up: RealImaginaryMass
Previous: 2.2 The signature of
Stefano Ansoldi
![]() -gauge the path integral for the partition function can be
rewritten, using (21) and going to euclidean space, as
-gauge the path integral for the partition function can be
rewritten, using (21) and going to euclidean space, as
![$\displaystyle \left [ \det \left( \Box + m _{\mathrm{A}} ^{2} \right)
\right] ^...
...2 \alpha} \int f ^{2} d ^{4} x} \times \det \left[
\partial ^{2} \right] \times$](img110.gif)
![$\displaystyle \times \, \exp \left\{ - \int \frac{d^4k}{(2\pi)^4} A _{\mu} (k)
...
...^{\nu} \right)} {k ^{2} - m _{\mathrm{A}} ^{2}} \right] A
_{\nu} (k) \right\} .$](img111.gif)