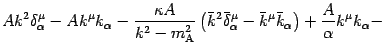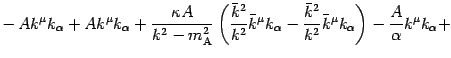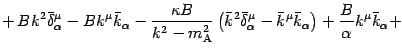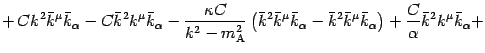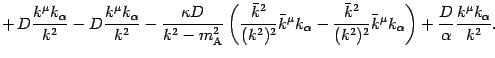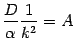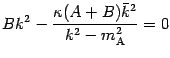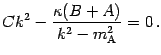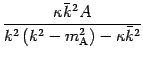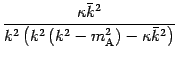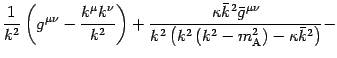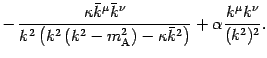

Next: C. Explicit computation of
Up: RealImaginaryMass
Previous: A. Eigenvectors and eigenvalues
B. Determination of the propagator
To determine the propagator in the covariant 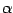 -gauge,
-gauge,
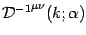 , with the four
dimensional quantities that are at our disposal we consider the
ansatz:
, with the four
dimensional quantities that are at our disposal we consider the
ansatz:
To determine the coefficients 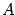 ,
, 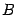 ,
, 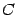 ,
, 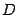 we can now compute
we can now compute
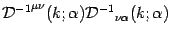 :
:
Now comparing terms with the same tensorial character
An independent subset of (four of) these gives (consistently with the
remaining equation) the final result for the coefficients:
so that we can finally write


Next: C. Explicit computation of
Up: RealImaginaryMass
Previous: A. Eigenvectors and eigenvalues
Stefano Ansoldi
![]() -gauge,
-gauge,
![]() , with the four
dimensional quantities that are at our disposal we consider the
ansatz:
, with the four
dimensional quantities that are at our disposal we consider the
ansatz:
![$\displaystyle \left[ \left( k ^{2} g ^{\mu \nu} - k ^{\mu} k ^{\nu} \right) -
\...
...\mu} \bar{k} ^{\nu} \right) +
\frac{1}{\alpha} k ^{\mu} k ^{\nu} \right] \times$](img190.gif)
![$\displaystyle \times \left[ A \left( g _{\nu \alpha} - \frac{k _{\nu} k
_{\alph...
..._{\nu} \bar{k} _{\alpha} + D \frac{k _{\nu} k _{\alpha}}{(k ^{2})
^{2}} \right]$](img191.gif)