

Next: 2.2 The signature of
Up: 2 General analysis of
Previous: 2 General analysis of
2.1 Path integral
An effective technical framework to investigate quantum fluctuations
around an external background configuration is provided by the Feynman
path integral formalism. The partition function(al) encoding the
dynamics of the interacting 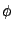 and
and 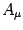 fields reads
fields reads
![\begin{displaymath}
Z \equiv \int [ {\mathcal{D}} \phi ] [ {\mathcal{D}} A ]
\exp\left\{ - \imath \int d ^{4} x {\mathcal{L}} \right\},
\end{displaymath}](img34.gif) |
(7) |
where
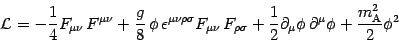 |
(8) |
and both the gauge fixing and ghost terms are, momentarily, understood
in the functional measure
![$[{\mathcal{D}} A]$](img36.gif) . For the sake of
generality, we assigned a non-vanishing mass to the pseudo scalar
field
. For the sake of
generality, we assigned a non-vanishing mass to the pseudo scalar
field 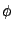 . Since the path integral (7) is gaussian in
. Since the path integral (7) is gaussian in
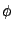 , the scalar field can be integrated away exactly, i.e.
, the scalar field can be integrated away exactly, i.e.
| |
|
![$\displaystyle \int [ {\mathcal{D}} \phi ] \exp \left\{ - \imath \int d ^{4}
x \...
... F
_{\rho \sigma} + \frac{m _{\mathrm{A}} ^{2}}{2} \phi ^{2} \right]
\right\} =$](img37.gif) |
|
| |
|
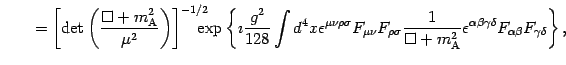 |
(9) |
where 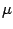 is a mass scale coming from the definition of the measure
is a mass scale coming from the definition of the measure
![$[ {\mathcal{D}} \phi ]$](img40.gif) . Integrating out the
. Integrating out the 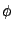 field induces a
non-local effective action for the
field induces a
non-local effective action for the 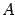 field. We stress that this
effective action, being obtained at the non-perturbative level,
takes into account (as an effective action for
field. We stress that this
effective action, being obtained at the non-perturbative level,
takes into account (as an effective action for 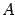 ) all the effects
due to the presence of the pseudoscalars at all perturbative
orders. This is a crucial difference with many of the previous works
on the subject. As is clear from (9), the resulting path
integral is quartic in
) all the effects
due to the presence of the pseudoscalars at all perturbative
orders. This is a crucial difference with many of the previous works
on the subject. As is clear from (9), the resulting path
integral is quartic in 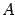 but, even if it cannot be computed in a
closed form, the background field method provides a reliable
approximation scheme to deal with this problem. We thus split
but, even if it cannot be computed in a
closed form, the background field method provides a reliable
approximation scheme to deal with this problem. We thus split 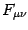 in the sum of a classical background
in the sum of a classical background
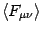 and a small fluctuation
and a small fluctuation 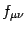 :
:
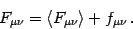 |
(10) |
In the case of a pure electric or a pure magnetic background we have
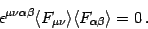 |
(11) |
Thus, expanding 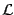 up to quadratic terms and dropping a
total divergence, we obtain for the effective lagrangian of the
fluctuations of the electromagnetic field
up to quadratic terms and dropping a
total divergence, we obtain for the effective lagrangian of the
fluctuations of the electromagnetic field
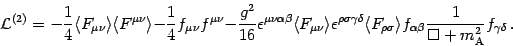 |
(12) |
As we will see in a while, there is an important sign difference
between the magnetic and the electric case.


Next: 2.2 The signature of
Up: 2 General analysis of
Previous: 2 General analysis of
Stefano Ansoldi
![]() and
and ![]() fields reads
fields reads