


Next: 4. Dynamics of the
Up: Membrane Vacuum as a
Previous: 2. The formalism
After the preparatory discussion of the previous section, we assign
to the field ![$\Psi [S]$](img5.gif) the following action
the following action
where, at present,
![$\oint [DS] \dots$](img39.gif) is a formal way to write the
functional sum over equivalence classes of closed surfaces with
respect to reparametrization invariance, and
is a formal way to write the
functional sum over equivalence classes of closed surfaces with
respect to reparametrization invariance, and
![$F _{\lambda \mu \nu \rho}= \partial _{ [ \mu} A _{\nu \rho \sigma]}$](img40.gif) is the gauge field strength
of the rank-three tensor gauge potential
is the gauge field strength
of the rank-three tensor gauge potential
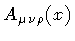 .
The shorthand
notation used in (8) is convenient but hides some essential
features of the action functional which are worth discussing at this
point. From our vantage point, the key property of the action
(8) is its invariance under the extended gauge transformation
.
The shorthand
notation used in (8) is convenient but hides some essential
features of the action functional which are worth discussing at this
point. From our vantage point, the key property of the action
(8) is its invariance under the extended gauge transformation
This transformation consists of an ``ordinary'' gauge term for
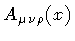 ,
which is defined over spacetime,
and a non local term for the phase of the membrane functional
,
which is defined over spacetime,
and a non local term for the phase of the membrane functional ![$\Psi [S]$](img5.gif) .
.
The second term in the action contains a spacetime integral which is
not explicitly shown in the expression (8). The reason is that a
free theory of surfaces is invariant under translations of the
center of mass
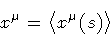 |
(11) |
so that the membrane action functional in (8)
contains the spacetime four-volume as the corresponding zero-mode
contribution. This translational invariance is broken by the coupling
to an ``external'' field
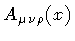 ,
in which case the four dimensional
zero-mode integral is no longer trivial [8]. It can be factored out
by inserting the ``unity operator'' [9]
,
in which case the four dimensional
zero-mode integral is no longer trivial [8]. It can be factored out
by inserting the ``unity operator'' [9]
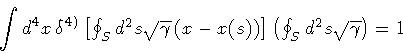 |
(12) |
into the functional integral. Then, we define the sum over surfaces
as a sum over all the surfaces with the center of mass in x, and
then we integrate over x:
All of the above applies to the quantum mechanical formulation of
surfaces interpreted as geometric objects. On more
physical grounds, membranes represent energy layers
characterized by a typical thickness, say
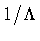 ,
which will be
determined later on.
To take into account the finite thickness of a physical
membrane, the singular delta-function which corresponds to the
``thin film approximation'', has to be smeared into a regular
function sharply peaked around
,
which will be
determined later on.
To take into account the finite thickness of a physical
membrane, the singular delta-function which corresponds to the
``thin film approximation'', has to be smeared into a regular
function sharply peaked around
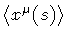 .
The
simplest representation for such a function is given by a
momentum space gaussian
.
The
simplest representation for such a function is given by a
momentum space gaussian
![\begin{displaymath}\delta ^{4)}
\left[ x - \langle x(s) \rangle \right]
\right...
...angle x ^{\mu} (s) \rangle)
-
k ^{2} / ( 2 \Lambda)
}
}
.
\end{displaymath}](img52.gif) |
(14) |
However, as long as we work at a distance scale much larger than
the membrane transverse dimension, we can approximate the physical
extended object with a geometrical surface. In what follows we
shall refer to the regularized delta-function only when it is
strictly necessary. With the above
prescriptions, the action (8)
can be written as the spacetime integral of a lagrangian density
![\begin{displaymath}{\mathcal{S}} [ \Psi ^{*} , \Psi ; A _{\mu \nu \rho}]
=
\in...
...ert
{\mathcal{D}} \Psi [S]
\Big \vert ^{2} \rangle
\right\}
\end{displaymath}](img53.gif) |
(15) |
and the interaction between the membrane field current and the
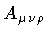 potential is described by
potential is described by
where g is the gauge coupling constant of dimension two in energy units.
As a classical ``charge'', it describes the strength of the
interaction among volume elements of the world-tube swept in spacetime by the
membrane evolution. In our functional field theory g enters as the
interaction constant between the membrane field current and the gauge
potential. Equation (16) exhibits a characteristic London form
which alerts us about the occurrence of non-trivial vacuum phases.
Indeed, the current implicitly defined in the last step in equation
(16), can be rewritten in the following form
where we have introduced the scalar field
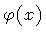
![\begin{displaymath}\varphi ^{2} (x)
\equiv
g ^{2}
\oint [ D x ^{\mu} (s) ]
\...
...le
)
-
k ^{2} / (2 \Lambda)
}
}
\vert \Psi[S] \vert ^{2}
\end{displaymath}](img64.gif) |
(18) |
which we interpret as the order parameter associated with
membrane condensation in the
same way that the Higgs field is the order parameter associated
with the boson condensation of point-like objects. In the ordinary
vacuum
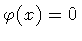 ,
i.e. there are no centers of mass, and
therefore no membranes. Alternatively, we define a vacuum
characterized by a constant ``density of centers of mass'',
,
i.e. there are no centers of mass, and
therefore no membranes. Alternatively, we define a vacuum
characterized by a constant ``density of centers of mass'',
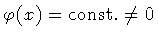 ,
as a membrane condensate.
,
as a membrane condensate.
We will show in Section 4 that the membrane condensate acts as a
superconductor upon the gauge potential,
turning
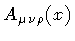 into a massive scalar field. The problem
of surface condensation is thus reduced to studying the distribution
of their representative, pointlike, centers of mass. Conversely, we
show in Section 5 that membrane condensation can be
driven by the
into a massive scalar field. The problem
of surface condensation is thus reduced to studying the distribution
of their representative, pointlike, centers of mass. Conversely, we
show in Section 5 that membrane condensation can be
driven by the
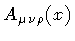 -field quantum corrections alone, and is
accounted for by an effective potential ascribed to the extended
object. This is Umezawa's self-consistency condition transplanted
in our own formalism.
-field quantum corrections alone, and is
accounted for by an effective potential ascribed to the extended
object. This is Umezawa's self-consistency condition transplanted
in our own formalism.



Next: 4. Dynamics of the
Up: Membrane Vacuum as a
Previous: 2. The formalism
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() the following action
the following action
![$\displaystyle \Psi [S]
\exp
\left(
i
\frac{g}{2}
\oint _{S} d y ^{\mu} \wedge d y ^{\nu}
\Lambda _{\mu \nu} (y)
\right)$](img42.gif)
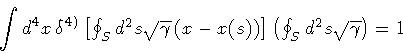
![$\displaystyle \oint [D S] ( \dots )$](img47.gif)
![$\displaystyle \int d ^{4} x
\oint [ D x ^{\mu} (s) ]
\delta ^{4)}
\left[ x - \langle x(s) \rangle \right]
( \dots )
\ ,$](img48.gif)
![$\displaystyle \int d ^{4} x
\oint [ D S _{x} ] ( \dots )$](img49.gif)
![\begin{displaymath}\delta ^{4)}
\left[ x - \langle x(s) \rangle \right]
\right...
...angle x ^{\mu} (s) \rangle)
-
k ^{2} / ( 2 \Lambda)
}
}
.
\end{displaymath}](img52.gif)
![\begin{displaymath}{\mathcal{S}} [ \Psi ^{*} , \Psi ; A _{\mu \nu \rho}]
=
\in...
...ert
{\mathcal{D}} \Psi [S]
\Big \vert ^{2} \rangle
\right\}
\end{displaymath}](img53.gif)
![\begin{displaymath}\varphi ^{2} (x)
\equiv
g ^{2}
\oint [ D x ^{\mu} (s) ]
\...
...le
)
-
k ^{2} / (2 \Lambda)
}
}
\vert \Psi[S] \vert ^{2}
\end{displaymath}](img64.gif)