


Next: 3. The action
Up: Membrane Vacuum as a
Previous: 1. Introduction
The picture of membrane superconductivity, as opposed to
vortex superconductivity, can be visualized as ``islands'' of
normal vacuum surrounded by a ``sea'' of massive
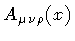 -quanta.
In general, the emergence of different vacuum
phases in the ground state of a physical system is accompanied
by the formation of boundary layers
between the various vacuum domains. In our approach, these
boundaries are approximated by geometrical manifolds of various
dimensionality (p-branes). This is the point where we depart
from Umezawa's approach: p-branes are introduced at the outset with
their own action functional, and therefore possess their own dynamics
independently of an underlying local field theory.
Classical bubble-dynamics has been studied in detail [4],
and this paper represents a tentative step toward the quantum
formulation. The paradigm of the quantum approach is a line field
theory introduced several years ago by Marshall and Ramond
as a basis for a second quantized formulation of closed string electrodynamics
[5]. We are interested in the case of relativistic,
spatially closed membranes whose history in spacetime is
represented by infinitely thin (1+2)-dimensional Lorentzian
submanifolds of Minkowski space (M). In a first quantized approach,
membrane coordinates and momenta become operators acting over an appropriate
space of states. However, the non linearity of the theory and the invariance
under reparametrizations
introduce severe problems in the first quantized formulation, e.g.
operator anomalies in the algebra of constraints. At least for closed
membranes, one can bypass these difficulties by considering a
field theory of geometric surfaces [6]. If we consider the abstract
space F of all possible bubble configurations, then we are led to consider
a field theory of quantum membranes in which the membrane field is a
reparametrization invariant, complex, functional of the two-surface S
which we assume to be the only boundary of the membrane
history. Our objective, then, is to introduce and discuss the action
which governs the evolution of quantum membranes regarded as 3-dimensional
timelike submanifolds of Minkowski space. To this end,
our first step is to introduce the 3-volume derivative
-quanta.
In general, the emergence of different vacuum
phases in the ground state of a physical system is accompanied
by the formation of boundary layers
between the various vacuum domains. In our approach, these
boundaries are approximated by geometrical manifolds of various
dimensionality (p-branes). This is the point where we depart
from Umezawa's approach: p-branes are introduced at the outset with
their own action functional, and therefore possess their own dynamics
independently of an underlying local field theory.
Classical bubble-dynamics has been studied in detail [4],
and this paper represents a tentative step toward the quantum
formulation. The paradigm of the quantum approach is a line field
theory introduced several years ago by Marshall and Ramond
as a basis for a second quantized formulation of closed string electrodynamics
[5]. We are interested in the case of relativistic,
spatially closed membranes whose history in spacetime is
represented by infinitely thin (1+2)-dimensional Lorentzian
submanifolds of Minkowski space (M). In a first quantized approach,
membrane coordinates and momenta become operators acting over an appropriate
space of states. However, the non linearity of the theory and the invariance
under reparametrizations
introduce severe problems in the first quantized formulation, e.g.
operator anomalies in the algebra of constraints. At least for closed
membranes, one can bypass these difficulties by considering a
field theory of geometric surfaces [6]. If we consider the abstract
space F of all possible bubble configurations, then we are led to consider
a field theory of quantum membranes in which the membrane field is a
reparametrization invariant, complex, functional of the two-surface S
which we assume to be the only boundary of the membrane
history. Our objective, then, is to introduce and discuss the action
which governs the evolution of quantum membranes regarded as 3-dimensional
timelike submanifolds of Minkowski space. To this end,
our first step is to introduce the 3-volume derivative
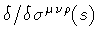 ,
which extends the notion of
``loop derivative'' introduced, some years ago, in the framework of the loop
formulation of gauge theories [7]. The underlying idea is
this: suppose we attach at a given point s of the surface S, an
infinitesimal, closed surface
,
which extends the notion of
``loop derivative'' introduced, some years ago, in the framework of the loop
formulation of gauge theories [7]. The underlying idea is
this: suppose we attach at a given point s of the surface S, an
infinitesimal, closed surface 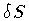 .
This procedure is equivalent to a
deformation of the initial shape of S in the neighborhood of s, thereby
changing the enclosed volume by an infinitesimal amount
.
This procedure is equivalent to a
deformation of the initial shape of S in the neighborhood of s, thereby
changing the enclosed volume by an infinitesimal amount 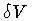 .
Then, we define the volume derivative of
.
Then, we define the volume derivative of ![$\Psi [S]$](img5.gif) through the relation
through the relation
![\begin{displaymath}\delta \Psi [S]
\equiv
\Psi [S \oplus \delta S]
-
\Psi [S...
...rho} (s)}
\,
d x ^{\mu} \wedge d x ^{\nu} \wedge d x ^{\rho}
\end{displaymath}](img6.gif) |
(1) |
in the limit of vanishing 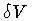 .
This definition is ``local''
to the extent that it involves a single point on the surface. For
the whole S , an averaging procedure is required
.
This definition is ``local''
to the extent that it involves a single point on the surface. For
the whole S , an averaging procedure is required
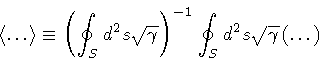 |
(2) |
where,
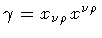 is the determinant of the metric induced over S
by the embedding
is the determinant of the metric induced over S
by the embedding
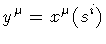 and
and
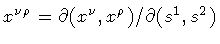 is the surface tangent
bi-vector. The volume derivative is related to the more familiar
functional variation
is the surface tangent
bi-vector. The volume derivative is related to the more familiar
functional variation
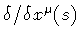 by the relation
by the relation
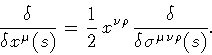 |
(3) |
Our second step towards the formulation of the membrane wave
equation, is to introduce the concept of
monodromy for the ![$\Psi [S]$](img5.gif) field, since this notion is
directly linked to the physical interpretation of the membrane field.
Our requirement is that
field, since this notion is
directly linked to the physical interpretation of the membrane field.
Our requirement is that
![$\Psi [S] \equiv A [S] e ^{i \Theta [S]}$](img13.gif) be a single valued functional of S, i.e. the phase
be a single valued functional of S, i.e. the phase
![\begin{displaymath}\Theta [S]
\equiv
\frac{1}{2}
\oint _{S} d x ^{\mu} \wedge d x ^{\nu}
\theta _{\mu \nu} (x)
\end{displaymath}](img14.gif) |
(4) |
can vary only by 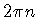 ,
n=1,2,...,
under transport along a ``loop'' in surface space. This condition
constitutes the basis of the analogy with a type-II superconductor.
In order to illustrate the precise meaning of this analogy, it is
convenient to interpret the motion of a bubble in the abstract space
F in which each point corresponds to a possible bubble
configuration. Then, the 3-volume derivative introduced above
represents the spacetime image of the generator of
translations in F-space and ``classical motion'' in F-space
corresponds to a continuous surface deformation in Minkowski space.
With this understanding, we define a ``line'' in F-space as a one-parameter
family of ``points'', i.e., surface configurations
,
n=1,2,...,
under transport along a ``loop'' in surface space. This condition
constitutes the basis of the analogy with a type-II superconductor.
In order to illustrate the precise meaning of this analogy, it is
convenient to interpret the motion of a bubble in the abstract space
F in which each point corresponds to a possible bubble
configuration. Then, the 3-volume derivative introduced above
represents the spacetime image of the generator of
translations in F-space and ``classical motion'' in F-space
corresponds to a continuous surface deformation in Minkowski space.
With this understanding, we define a ``line'' in F-space as a one-parameter
family of ``points'', i.e., surface configurations
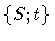 in physical
space. Let each surface in the family be represented by the embedding equation
in physical
space. Let each surface in the family be represented by the embedding equation
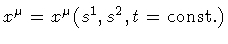 ,
where
t is the real parameter labelling in a one-to-one way
each surface of the family, so that
,
where
t is the real parameter labelling in a one-to-one way
each surface of the family, so that
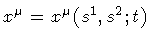 represents
the embedding of the whole family. However, the same relation
can be interpreted as the embedding of a single three-surface whose
t =const.
sections reproduce each surface of the family.
In a similar way, we define a ``loop'' of surfaces as a one-parameter
family of surfaces in which the first and the last are identified.
Then, according to our definition of
volume derivative as the spacetime image of the translation
generator in surface space, we define the circulation of
represents
the embedding of the whole family. However, the same relation
can be interpreted as the embedding of a single three-surface whose
t =const.
sections reproduce each surface of the family.
In a similar way, we define a ``loop'' of surfaces as a one-parameter
family of surfaces in which the first and the last are identified.
Then, according to our definition of
volume derivative as the spacetime image of the translation
generator in surface space, we define the circulation of
![$\Theta [S]$](img19.gif) as the
flux of the covariant curl of
as the
flux of the covariant curl of
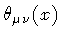 :
:
where
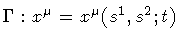 ,
with
,
with
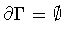 represents the spacetime image of the
integration path in surface space.
represents the spacetime image of the
integration path in surface space.
Finally, we define a vortex line in surface space, as a one-parameter
family of surfaces
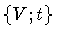 for which the amplitude of the membrane field
vanishes, i.e.
for which the amplitude of the membrane field
vanishes, i.e.
![$\vert \Psi [ V _{t} ] \vert = 0$](img28.gif) .
In order to avoid boundary terms
and thus simplify calculations, we assume that the vortex line is closed.
In other words, the spacetime image of the vortex line is a compact three
surface without boundary that we shall denote by
.
In order to avoid boundary terms
and thus simplify calculations, we assume that the vortex line is closed.
In other words, the spacetime image of the vortex line is a compact three
surface without boundary that we shall denote by
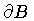 .
.
Suppose the test loop of surfaces
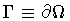 surrounds the vortex line
surrounds the vortex line
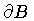 ,
then
the monodromy of
,
then
the monodromy of ![$\Psi [S]$](img5.gif) implies the quantization condition :
implies the quantization condition :
![\begin{displaymath}\Delta \Theta [S]
=
\frac{1}{3!}
\oint _{\Gamma} d x ^{\mu...
...\theta _{\nu \rho ]}
=
2 \pi n
\ , \quad
n = 1 , 2 , \dots
\end{displaymath}](img31.gif) |
(6) |
If the flux (6) is quantized, then 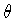 is a singular function
within B. Indeed, using Stokes' theorem, we rewrite (6) as
is a singular function
within B. Indeed, using Stokes' theorem, we rewrite (6) as
The ``Bag'' B is the domain of singularity of the phase 2-form
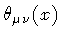 and represents the spacetime image of the
``vortex interior''.
and represents the spacetime image of the
``vortex interior''.



Next: 3. The action
Up: Membrane Vacuum as a
Previous: 1. Introduction
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() -quanta.
In general, the emergence of different vacuum
phases in the ground state of a physical system is accompanied
by the formation of boundary layers
between the various vacuum domains. In our approach, these
boundaries are approximated by geometrical manifolds of various
dimensionality (p-branes). This is the point where we depart
from Umezawa's approach: p-branes are introduced at the outset with
their own action functional, and therefore possess their own dynamics
independently of an underlying local field theory.
Classical bubble-dynamics has been studied in detail [4],
and this paper represents a tentative step toward the quantum
formulation. The paradigm of the quantum approach is a line field
theory introduced several years ago by Marshall and Ramond
as a basis for a second quantized formulation of closed string electrodynamics
[5]. We are interested in the case of relativistic,
spatially closed membranes whose history in spacetime is
represented by infinitely thin (1+2)-dimensional Lorentzian
submanifolds of Minkowski space (M). In a first quantized approach,
membrane coordinates and momenta become operators acting over an appropriate
space of states. However, the non linearity of the theory and the invariance
under reparametrizations
introduce severe problems in the first quantized formulation, e.g.
operator anomalies in the algebra of constraints. At least for closed
membranes, one can bypass these difficulties by considering a
field theory of geometric surfaces [6]. If we consider the abstract
space F of all possible bubble configurations, then we are led to consider
a field theory of quantum membranes in which the membrane field is a
reparametrization invariant, complex, functional of the two-surface S
which we assume to be the only boundary of the membrane
history. Our objective, then, is to introduce and discuss the action
which governs the evolution of quantum membranes regarded as 3-dimensional
timelike submanifolds of Minkowski space. To this end,
our first step is to introduce the 3-volume derivative
-quanta.
In general, the emergence of different vacuum
phases in the ground state of a physical system is accompanied
by the formation of boundary layers
between the various vacuum domains. In our approach, these
boundaries are approximated by geometrical manifolds of various
dimensionality (p-branes). This is the point where we depart
from Umezawa's approach: p-branes are introduced at the outset with
their own action functional, and therefore possess their own dynamics
independently of an underlying local field theory.
Classical bubble-dynamics has been studied in detail [4],
and this paper represents a tentative step toward the quantum
formulation. The paradigm of the quantum approach is a line field
theory introduced several years ago by Marshall and Ramond
as a basis for a second quantized formulation of closed string electrodynamics
[5]. We are interested in the case of relativistic,
spatially closed membranes whose history in spacetime is
represented by infinitely thin (1+2)-dimensional Lorentzian
submanifolds of Minkowski space (M). In a first quantized approach,
membrane coordinates and momenta become operators acting over an appropriate
space of states. However, the non linearity of the theory and the invariance
under reparametrizations
introduce severe problems in the first quantized formulation, e.g.
operator anomalies in the algebra of constraints. At least for closed
membranes, one can bypass these difficulties by considering a
field theory of geometric surfaces [6]. If we consider the abstract
space F of all possible bubble configurations, then we are led to consider
a field theory of quantum membranes in which the membrane field is a
reparametrization invariant, complex, functional of the two-surface S
which we assume to be the only boundary of the membrane
history. Our objective, then, is to introduce and discuss the action
which governs the evolution of quantum membranes regarded as 3-dimensional
timelike submanifolds of Minkowski space. To this end,
our first step is to introduce the 3-volume derivative
![]() ,
which extends the notion of
``loop derivative'' introduced, some years ago, in the framework of the loop
formulation of gauge theories [7]. The underlying idea is
this: suppose we attach at a given point s of the surface S, an
infinitesimal, closed surface
,
which extends the notion of
``loop derivative'' introduced, some years ago, in the framework of the loop
formulation of gauge theories [7]. The underlying idea is
this: suppose we attach at a given point s of the surface S, an
infinitesimal, closed surface ![]() .
This procedure is equivalent to a
deformation of the initial shape of S in the neighborhood of s, thereby
changing the enclosed volume by an infinitesimal amount
.
This procedure is equivalent to a
deformation of the initial shape of S in the neighborhood of s, thereby
changing the enclosed volume by an infinitesimal amount ![]() .
Then, we define the volume derivative of
.
Then, we define the volume derivative of ![]() through the relation
through the relation
![\begin{displaymath}\delta \Psi [S]
\equiv
\Psi [S \oplus \delta S]
-
\Psi [S...
...rho} (s)}
\,
d x ^{\mu} \wedge d x ^{\nu} \wedge d x ^{\rho}
\end{displaymath}](img6.gif)
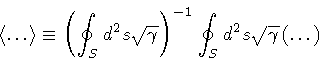
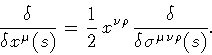
![\begin{displaymath}\Theta [S]
\equiv
\frac{1}{2}
\oint _{S} d x ^{\mu} \wedge d x ^{\nu}
\theta _{\mu \nu} (x)
\end{displaymath}](img14.gif)