


Next: 4. Inflationary bubble nucleation
Up: Effective Dynamics of Self-Gravitating
Previous: 2. False vacuum decay
3. ``Minkowski pair'' creation
The simplest example of gravitational vacuum fluctuation is given
by the spontaneous nucleation of a vanishing mass-energy shell in
Minkowski
spacetime. Despite the triviality of both the internal and external
geometries,
the dynamics of such a process is nonetheless affected by the
unavoidable ambiguities and technical problems of quantum gravity.
To circumvent all these difficulties, one usually employs a
semi-classical
model obtained by gluing together two Minkowski metrics along the
bubble
trajectory .
In our approach, the steps are as
follows. The signs of
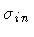 ,
,
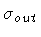 are
fixed by the matching condition
are
fixed by the matching condition
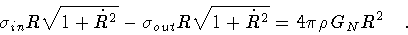 |
(14) |
For a positive surface tension we have
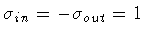 ,
otherwise the two spacetime domains cannot be glued
together. The resulting geometry represents the limiting
configuration
of vanishing cosmological constant and Schwarzschild mass discussed
in appendix D of Ref. [11]. This is a closed universe formed
by two
compact spherical regions of flat spacetime.
The shell equation of motion obtained by squaring (14) is
,
otherwise the two spacetime domains cannot be glued
together. The resulting geometry represents the limiting
configuration
of vanishing cosmological constant and Schwarzschild mass discussed
in appendix D of Ref. [11]. This is a closed universe formed
by two
compact spherical regions of flat spacetime.
The shell equation of motion obtained by squaring (14) is
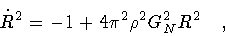 |
(15) |
and admits only bounce solutions irrespective of the sign of 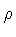 .
In our case
.
In our case
Note that, in order to recover Eq.(18) from the general
formula (7),
one must carefully assign the phases of the complexified functions
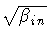 ,
,
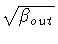 in the analytically
extended Schwarzschild manifold, and only then one may consider the
limit of vanishing Schwarzschild mass.
This is because the effective hamiltonian
(7) is actually a complex function when considered on the
maximally analytic extension of the underlying spacetime manifold.
This and other technical problems will be discussed elsewhere. Presently,
however, it is worth observing that
the kinetic term, obtained by expanding ``
in the analytically
extended Schwarzschild manifold, and only then one may consider the
limit of vanishing Schwarzschild mass.
This is because the effective hamiltonian
(7) is actually a complex function when considered on the
maximally analytic extension of the underlying spacetime manifold.
This and other technical problems will be discussed elsewhere. Presently,
however, it is worth observing that
the kinetic term, obtained by expanding ``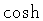 '' up to second
order, is negative. Therefore,
'' up to second
order, is negative. Therefore,
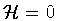 is the classical
equation of motion of a (positive kinetic energy) particle in the
reversed potential
is the classical
equation of motion of a (positive kinetic energy) particle in the
reversed potential
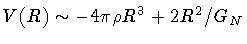 .
This
potential
constitutes an effective barrier for the ``particle'' motion and
explains the absence of a discrete spectrum of stationary quantum
states. The classical dynamics of
this type of domain wall has been discussed in Ref. [15] with
special emphasis on the repulsive character of the
resulting gravitational field. In our formulation, this repulsive
effect is plainly exhibited by the potential above.
We propose to associate the expected quantum mechanical
``leakage'' through the potential barrier with the process of
``universe creation'' by quantum tunneling from nothing.
In order to give substance to this interpretation, one needs to
compute the corresponding transmission coefficient, and, in order to
perform this calculation, we rotate
the dynamical quantities to imaginary time:
.
This
potential
constitutes an effective barrier for the ``particle'' motion and
explains the absence of a discrete spectrum of stationary quantum
states. The classical dynamics of
this type of domain wall has been discussed in Ref. [15] with
special emphasis on the repulsive character of the
resulting gravitational field. In our formulation, this repulsive
effect is plainly exhibited by the potential above.
We propose to associate the expected quantum mechanical
``leakage'' through the potential barrier with the process of
``universe creation'' by quantum tunneling from nothing.
In order to give substance to this interpretation, one needs to
compute the corresponding transmission coefficient, and, in order to
perform this calculation, we rotate
the dynamical quantities to imaginary time:
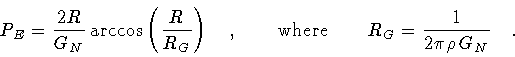 |
(19) |
This gives, for the nucleation coefficient
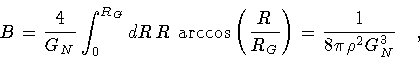 |
(20) |
in agreement with the bounce calculation of Ref. [12].
In the case of negative surface tension the calculation proceeds
along the same steps outlined above, but with
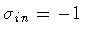 ,
,
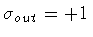 .
The resulting geometry is the limiting case
of a ``surgically'' constructed Schwarzschild wormhole, when the
mass is sent
to zero [3]. However, any constant time section of the
resulting
spacetime has infinite volume. Thus, this second type of
``Minkowski pair'' does not correspond to
a compact object and cannot be nucleated quantum mechanically from
``nothing''.
.
The resulting geometry is the limiting case
of a ``surgically'' constructed Schwarzschild wormhole, when the
mass is sent
to zero [3]. However, any constant time section of the
resulting
spacetime has infinite volume. Thus, this second type of
``Minkowski pair'' does not correspond to
a compact object and cannot be nucleated quantum mechanically from
``nothing''.



Next: 4. Inflationary bubble nucleation
Up: Effective Dynamics of Self-Gravitating
Previous: 2. False vacuum decay
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() ,
,
![]() are
fixed by the matching condition
are
fixed by the matching condition
![]() ,
,
![]() .
The resulting geometry is the limiting case
of a ``surgically'' constructed Schwarzschild wormhole, when the
mass is sent
to zero [3]. However, any constant time section of the
resulting
spacetime has infinite volume. Thus, this second type of
``Minkowski pair'' does not correspond to
a compact object and cannot be nucleated quantum mechanically from
``nothing''.
.
The resulting geometry is the limiting case
of a ``surgically'' constructed Schwarzschild wormhole, when the
mass is sent
to zero [3]. However, any constant time section of the
resulting
spacetime has infinite volume. Thus, this second type of
``Minkowski pair'' does not correspond to
a compact object and cannot be nucleated quantum mechanically from
``nothing''.