


Next: 3. ``Minkowski pair'' creation
Up: Effective Dynamics of Self-Gravitating
Previous: 1. Introduction
2. False vacuum decay
Our effective description is general enough to include
bubble dynamics in the absence of gravity as well. The limit
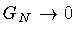 represent not only a necessary consistency check of our model, but also
a worth investigating special case by itself.
represent not only a necessary consistency check of our model, but also
a worth investigating special case by itself.
The correct limiting procedure requires to express the two cosmological
constants in terms of the corresponding vacuum energy densities
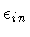 ,
,
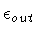 :
:
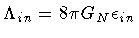 ,
,
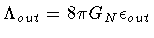 .
In a single Minkowski domain
.
In a single Minkowski domain
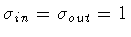 .
Then, by expanding
.
Then, by expanding
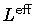 up to the first order in
up to the first order in
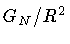 we get
we get
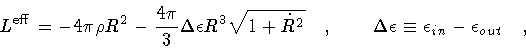 |
(8) |
and represents the minisuperspace approximation of the gauge action
for the membrane
where, 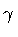 is the determinant of the induced metric
on the
is the determinant of the induced metric
on the 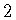 -brane world tube
-brane world tube
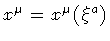 ,
,
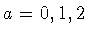 ,
and
,
and
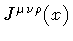 is the
is the 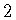 -brane current.
The last term in (9) is a total divergence ensuring
that variations of the gauge potential
-brane current.
The last term in (9) is a total divergence ensuring
that variations of the gauge potential
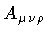 will not produce unusual boundary terms due to the presence of the
will not produce unusual boundary terms due to the presence of the
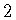 -brane world tube.
The corresponding hamiltonian is
-brane world tube.
The corresponding hamiltonian is
The classical trajectories describing true vacuum bubbles
are solutions of the hamiltonian constraint
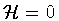 stating that the total mass energy of a
vacuum bubble is
vanishing. From equation (10) we see that
classical solutions, corresponding to positive surface
tension bubbles, are allowed only if
stating that the total mass energy of a
vacuum bubble is
vanishing. From equation (10) we see that
classical solutions, corresponding to positive surface
tension bubbles, are allowed only if
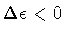 ,
i.e.
the internal energy density (of the true vacuum) must be smaller
than the external energy density (of the false vacuum), the net amount
of energy released in the transition being converted into (positive)
kinetic energy of the bubble wall.
The semi-classical picture of the true vacuum domain nucleation
corresponds to a classically forbidden motion.
The classically unphysical tunneling trajectory
is a solutions of the euclidean, equation of motion
obtained via the Wick rotation
,
i.e.
the internal energy density (of the true vacuum) must be smaller
than the external energy density (of the false vacuum), the net amount
of energy released in the transition being converted into (positive)
kinetic energy of the bubble wall.
The semi-classical picture of the true vacuum domain nucleation
corresponds to a classically forbidden motion.
The classically unphysical tunneling trajectory
is a solutions of the euclidean, equation of motion
obtained via the Wick rotation
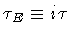 ,
,
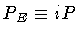
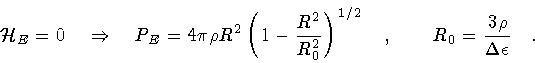 |
(12) |
Then, we can use the classical solution (12)
for 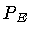 in the WKB integral
for the calculation of the nucleation probability through tunnel effect:
in the WKB integral
for the calculation of the nucleation probability through tunnel effect:
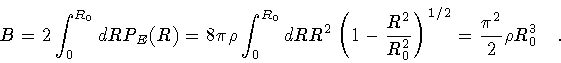 |
(13) |
The usual result (13) is in agreement with the Coleman-DeLuccia
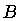 decay coefficient [18].
decay coefficient [18].



Next: 3. ``Minkowski pair'' creation
Up: Effective Dynamics of Self-Gravitating
Previous: 1. Introduction
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() represent not only a necessary consistency check of our model, but also
a worth investigating special case by itself.
represent not only a necessary consistency check of our model, but also
a worth investigating special case by itself.
![]() ,
,
![]() :
:
![]() ,
,
![]() .
In a single Minkowski domain
.
In a single Minkowski domain
![]() .
Then, by expanding
.
Then, by expanding
![]() up to the first order in
up to the first order in
![]() we get
we get