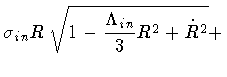 |
|||
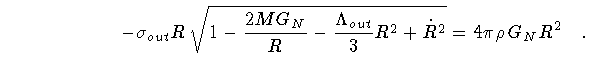 |
(1) |
The aim of this
communication is to suggest an effective approach to the
dynamics of spherically symmetric,
self-gravitating objects that
may arise, evolve and die in the spacetime foam. Among these
``objects'', somehow, there is the universe in which we live, and
therefore the study of such fluctuations hardly needs a
justification. In order to give some analytical substance to this
qualitative
picture, we envisage the spacetime foam as an
ensemble of vacuum bubbles, or
cells of spacetime, each characterized by its own geometric
phase
and vacuum energy density. In principle each cell may behave as a
black hole,
a wormhole, an inflationary bubble, etc., depending on the matching
conditions on the neighboring cells [8]. Thus, a useful starting
point for our present discussion, is the
general matching equation between the internal
and external metrics of a self-gravitating,
spherically symmetric bubble [9]
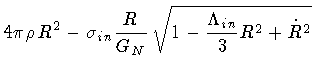 |
|||
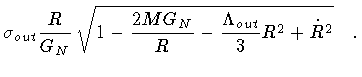 |
(2) |
The inverse Legendre transform (4) leads to the
effective lagrangian we are looking for
Note that the hamiltonian (7) involves a square root
operation in analogy to the familiar expression of the
energy of a relativistic point particle.
In our case the coefficient of the square root depends on
![]() in order to be consistent with the classical
equation of motion (1). The opposite sign
is classically meaningless. However, since we are dealing with a
relativistic
system, both positive and negative energies become physically
relevant
at the quantum level. This leads us to a broader interpretation
of spacetime foam as a ``Dirac sea of extended objects'', in which
not only wormholes, but also black holes and vacuum bubbles are
continuously created and destroyed as zero-point energy
fluctuations in the gravitational quantum vacuum. As a matter of
fact, the effective lagrangian (6), (or the effective
hamiltonian (7)), encodes the dynamics of a
four-parameter (
in order to be consistent with the classical
equation of motion (1). The opposite sign
is classically meaningless. However, since we are dealing with a
relativistic
system, both positive and negative energies become physically
relevant
at the quantum level. This leads us to a broader interpretation
of spacetime foam as a ``Dirac sea of extended objects'', in which
not only wormholes, but also black holes and vacuum bubbles are
continuously created and destroyed as zero-point energy
fluctuations in the gravitational quantum vacuum. As a matter of
fact, the effective lagrangian (6), (or the effective
hamiltonian (7)), encodes the dynamics of a
four-parameter (![]() ,
,
![]() ,
,
![]() ,
, ![]() ) family
of spherically symmetric, classical solutions of the self-gravitating
bubble equation of motion. Furthermore, the results (6)
and (7) can be extended in a straightforward manner to an even
larger family of solutions by endowing the internal geometry with a
non-vanishing Schwarzschild mass term
) family
of spherically symmetric, classical solutions of the self-gravitating
bubble equation of motion. Furthermore, the results (6)
and (7) can be extended in a straightforward manner to an even
larger family of solutions by endowing the internal geometry with a
non-vanishing Schwarzschild mass term
![]() ,
or the external geometry with an electric charge.
,
or the external geometry with an electric charge.
The spacetime foam models currently available in the literature
focus essentially on the Schwarzschild metric
(see, however, Ref. [2]), and correspond to the sector ![]() of our family of classical solutions.
For instance, in the sub-sector
of our family of classical solutions.
For instance, in the sub-sector ![]() ,
,
![]() ,
,
![]() ,
one finds the vacuum bubbles discussed
in Ref. [11]. In particular, we recall the type E
trajectories with
,
one finds the vacuum bubbles discussed
in Ref. [11]. In particular, we recall the type E
trajectories with
![]() ,
listed in the same reference, because
they give rise to baby-universes connected through wormholes to
the parent universe. The characteristics of those trajectories are
instrumental to our discussion in Section 4.
,
listed in the same reference, because
they give rise to baby-universes connected through wormholes to
the parent universe. The characteristics of those trajectories are
instrumental to our discussion in Section 4.
Other types of ``foam-like'' solutions belong to the subsector
![]() .
They include the ``surgical''
Schwarzschild-Schwarzschild wormholes [3], and the
``hollow'' Minkowski-Schwarzschild wormholes [4],
[12], while the region
.
They include the ``surgical''
Schwarzschild-Schwarzschild wormholes [3], and the
``hollow'' Minkowski-Schwarzschild wormholes [4],
[12], while the region ![]() of the same subsector
contains the traversable wormholes, i.e. wormholes whose
throats can be
crossed by timelike observers. In this connection, note that in our
membrane model a
negative tension plays the same role as the negative energy density
of the more conventional wormholes made out of ``dust'': it
provides the ``repulsive force'' required to oppose the
gravitational collapse of the throat [13]. The explicit
correspondence between negative energy density and surface tension
is provided by the simple
relation:
of the same subsector
contains the traversable wormholes, i.e. wormholes whose
throats can be
crossed by timelike observers. In this connection, note that in our
membrane model a
negative tension plays the same role as the negative energy density
of the more conventional wormholes made out of ``dust'': it
provides the ``repulsive force'' required to oppose the
gravitational collapse of the throat [13]. The explicit
correspondence between negative energy density and surface tension
is provided by the simple
relation:
![]() .
However, while the negative energy density of dusty wormholes is
ascribed to some kind of exotic matter [13], or to
gravitational vacuum polarization [14], we suggest
to interpret membranes with negative tension as boundary layers
between different physical vacua as suggested, for instance, by the
existence of normal and confining vacua in QCD. More about negative
energy density later.
.
However, while the negative energy density of dusty wormholes is
ascribed to some kind of exotic matter [13], or to
gravitational vacuum polarization [14], we suggest
to interpret membranes with negative tension as boundary layers
between different physical vacua as suggested, for instance, by the
existence of normal and confining vacua in QCD. More about negative
energy density later.
In section 2 we show that in the flat spacetime limit, i.e. for
![]() ,
the resulting lagrangian can be used to compute
the false vacuum decay amplitude in ordinary quantum field theory.
,
the resulting lagrangian can be used to compute
the false vacuum decay amplitude in ordinary quantum field theory.
In sections 3 and 4,
as an explicit application of our general
method, we shall study two examples of gravitational fluctuations in
the sector
![]() ,
which correspond to
vacuum bubbles. Their discussion and comparison with the
existing literature on the subject provide an excellent
testing ground for the validity of our approach.
,
which correspond to
vacuum bubbles. Their discussion and comparison with the
existing literature on the subject provide an excellent
testing ground for the validity of our approach.
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY