- ...http://www-dft.ts.infn.it/ ansoldi1
- E-mail address:
ansoldi@trieste.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formalism2
- But see also [8] and references
therein for a complementary approach which also tackles the issue of stability.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
shell3
- To avoid any possible
confusion, in what follows we are going to use
square brackets only with this meaning, according to
the following definition.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dynamics4
- We denote with an overbar quantities,
let us say
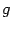 ,
which are function of the rescaled radial coordinate
,
which are function of the rescaled radial coordinate 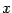 , although in
many cases we have
, although in
many cases we have
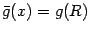 . For the sake of
precision, note that
. For the sake of
precision, note that
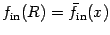 ,
,
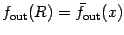 ,
,
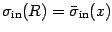 ,
,
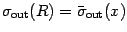 ,
and
,
and
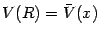 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... trajectory5
- Nevertheless
it equals
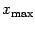 for
for
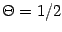 .
This is an interesting limiting situation in the case of
tunnelling across the potential barrier, which will be discussed elsewhere.
.
This is an interesting limiting situation in the case of
tunnelling across the potential barrier, which will be discussed elsewhere.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... of6
- We work
in units where
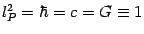 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... barrier7
- This
will be the topic of a forthcoming paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... properties8
- We define
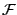 ,
, 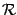 and
and 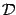 according to the first two
according to the first two 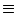 's of the equation
below.
's of the equation
below.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.