2 Preliminaries

In this section we define the system, motivate the settings under which we study its classical and semiclassical dynamics and recall some useful results and definitions.

Let us thus start with the geometrodynamical framework, by considering two spacetime domains joined along a spherically symmetric timelike shell. We assume, for the region we shall call the interior, a geometry of the de Sitter type [68,69,70] (we denote with $H$ the cosmological horizon), so that the metric in static coordinates is:

$$g _{\mathrm{in}} ^{\mu \nu} = \mathrm{diag} \left( f _{\mathrm{in}} (r) , f _{\mathrm{in}} ^{-1} (r) , r^{2} , r^{2} \sin \theta \right)$$ (1)

$$f _{\mathrm{in}} (r) = 1 - \frac{r ^{2}}{H ^{2}} .$$

For the exterior region we choose a spacetime of the Reißner-Nordström type [71,72,70], with metric given by

$$g _{\mathrm{out}} ^{\mu \nu} = \mathrm{diag} \left( f _{\mathrm{out}} (r) , f _{\mathrm{out}} ^{-1} (r) , r^{2} , r^{2} \sin \theta \right)$$ (2)

$$f _{\mathrm{out}} (r) = 1 - \frac{2 M}{r} + \frac{Q ^{2}}{r ^{2}} ,$$

$M$ being the Schwarzschild mass and $Q$ the electric charge. Furthermore we join the two regions along the timelike trajectory of a spherical dust shell of constant total mass-energy $m$.

As is well known [1,2] the dynamics of the compound gravitational system is encoded in Israel's junction conditions: they match the jump in the extrinsic curvature due to the different spacetime geometries on the two sides of the shell surface and the (singular) stress-energy tensor of the shell itself. Under the simplifying assumption of spherical symmetry considered here, it is possible to reduce them to the single scalar equation [73,74]

$$\left[ \sigma \beta \right] = \frac{m}{R} ,$$ (3)

where as customary we use square brackets as a shorthand for the jump of the enclosed quantity in the passage from the ``in'' to the ``out'' domain across the shell³, i.e.

$$\left[ X \right] := X _{\mathrm{in}} - X _{\mathrm{out}} ,$$

and

$$\left( \sigma \beta \right) _{\mathrm{in}} := \sigma _{\mathrm{in}} \beta _{\mathrm{in}} = \sigma _{\mathrm{in}} \sqrt{\dot{R} ^{2} + 1 - \frac{R ^{2}}{H ^{2}}}$$

$$\left( \sigma \beta \right) _{\mathrm{out}} := \sigma _{\mathrm{out}} \beta _{\mathrm{out}} = \sigma _{\mathrm{out}} \sqrt{\dot{R} ^{2} + 1 - \frac{2 M}{R} + \frac{Q ^{2}}{R ^{2}}} .$$

In the above expressions $R = R ( \tau )$ is the shell radius expressed as a function of the proper time $\tau$ of an observer co-moving with the shell and we denote with an over-dot the (total) derivative with respect to $\tau$.

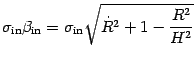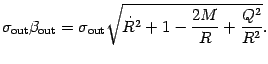From the general theory of shell dynamics, we know that the signs of the radicals do matter, being related both to the side of the maximally extended diagram for the spacetime manifold, which is crossed by the trajectory of the shell [64], and to the direction of the outward (i.e toward increasing radius) pointing normal to the shell surface [1,2]. This is the reason why they are denoted explicitly by $\sigma _{\mathrm{in}/\mathrm{out}}$. Their values can be analytically determined thanks to the results [73,74]

$$\sigma _{\mathrm{in}} = \sigma _{\mathrm{in}} (R) = - \mathrm{Sign} \left\{ m \left( \frac{R ^{4}}{H ^{2}} - 2 M R + Q ^{2} - m ^{2} \right) \right\}$$ (4)

$$\sigma _{\mathrm{out}} = \sigma _{\mathrm{out}} (R) = - \mathrm{Sign} \left\{ m \left( \frac{R ^{4}}{H ^{2}} - 2 M R + Q ^{2} + m ^{2} \right) \right\} ,$$ (5)

which can be obtained by properly squaring the junction condition (3).

Following the notation of reference [73] we know that the junction condition (3) can be derived as the Superhamiltonian constraint for the system, where the corresponding Superhamiltonian is then nothing but

$${\mathcal{H}} = P \dot{R} - {\mathcal{L}} = R \left[ \sigma \beta \right] - m ,$$ (6)

${\mathcal{L}}$ being the Lagrangian density

$${\mathcal{L}} = m - R \left\{ \left[ \sigma \beta -... ...{R}}{\sigma \beta - \dot{R}} \right\vert \right] \right\}$$ (7)

and $P$ being the conjugate momentum to the canonical variable $R$:

$$P = \frac{\partial {\mathcal{L}}}{\partial \dot{R}} = -... ...}{\sigma \beta - \dot{R}} \right\vert \right] \right\} .$$ (8)

The dynamics of the system can be studied with the help of an effective equation of motion, which is useful in removing the square roots in (3) and can be put in the form of a classical one-dimensional dynamical problem, the motion of an effective particle of unitary mass and vanishing total energy [64,75]

$$\dot{R} ^{2} + V (R) = 0$$ (9)

in a potential given by

$$V (R) = - \frac{ R ^{8} - 4 H^{2} M R ^{5} + 2 H ^{2} (m ^{2} + Q ^{2}) R ^{4} } {4 m ^{2} H ^{2} R ^{2}}$$

$$\qquad - \frac{ 4 H ^{4} (M ^{2} - m ^{2}) R ^{2} + 4 H ^{4} M (m ^{2} - Q ^{2}) R + H ^{4} (m ^{2} - Q ^{2}) ^{2} } {4 m ^{2} H ^{2} R ^{2}} .$$ (10)

To evaluate the classical action along a classically allowed trajectory, we need an expression for the effective momentum $P$ evaluated along the same trajectory. Thus we have to substitute for the $\dot{R}$ dependence in (8) and using in this procedure relation (9) we get

$$P (R) = - R \tanh ^{-1} \left\{ \left( \frac{2 m H ^{2} R \sqrt{- V (R)}}... ...H^{2} M R + H ^{2} \left( Q ^{2} - m ^{2} \right) } \right) ^{s (r)} \right\} ,$$ (11)

$$\mathrm{with} \quad s (r) = \mathrm{Sign} \left\{ \left( 1 - \fra... ...2}} \right) \left( 1 - \frac{2 M}{R} + \frac{Q ^{2}}{R ^{2}} \right) \right\} .$$

We can now use the above result to compute the action along a classically allowed trajectory, having turning points at $R _{1}$ and $R _{2}$, since

$$S _{\mathrm{classical}} = 2 \int _{R _{1}} ^{R _{2}} P (R) \mathrm{d} R ,$$ (12)

and then implement a semiclassical quantization scheme a la Bohr-Sommerfeld, by considering allowed quantum states to have the action as an integer multiple of the elementary quantum [76] $l _{\mathrm{P}} ^{2} \equiv \hbar \equiv 1$:

$$S _{\mathrm{classical}} = n , \quad n = 1 , 2 , \dots .$$ (13)

To successfully complete this task we need in first place an analysis of the allowed bounded classical trajectories, which we will perform in the next section.

Before embarking this program, let us shortly comment about the semiclassical quantization procedure outlined above. There are indeed many different approaches for the quantization of gravitational systems, and it is not often clear which should be the preferred one. Moreover, deep ideas have already been discussed to a great extent in the literature cited above. It is not the goal of this paper to address this fundamental problem, but we think it is important to give a short account about the reliability of the results that will be derived in what follows. In particular a formalism using expression (11), but evaluated along a classically forbidden trajectory, has already been successfully used in [77] and [73] to reproduce some well known results about vacuum decay and the influence of gravity on it, already studied in the seminal papers by Coleman and de Luccia [78] and by Parke [79]. Moreover, as already noted by Sommerfeld in the days of the early development of Quantum Mechanics [76], the quantization condition (13) is ``particularly valuable, for it could be applied both to relativistic and non-relativistic systems''. Thus, we think that the above considerations justify our tentative approach, in which the semiclassical quantization condition is applied, through an already tested procedure, to a classically well-know gravitational system.