

Next: 3 Tunnelling
Up: Vacuum decay by p-branes
Previous: 1 Introduction
The stress-energy tensor for a distribution of matter localized on
an hypersurface  (the
(the 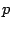 -brane we mentioned above)
can be written in the form
-brane we mentioned above)
can be written in the form
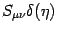 ,
where
,
where 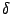 is a Dirac delta, and
is a Dirac delta, and 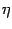 can be thought as
a transverse coordinate to
can be thought as
a transverse coordinate to 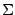 .
In
.
In 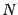 -dimensional General Relativity it is possible to write down
the equations of motion for this infinitesimally thin distribution of
matter by splitting Einstein equations in the tangential and
transverse part (see [4] for the
-dimensional General Relativity it is possible to write down
the equations of motion for this infinitesimally thin distribution of
matter by splitting Einstein equations in the tangential and
transverse part (see [4] for the 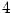 -dimensional case; it
can be extended to higher dimensions). Israel junction conditions, then, are
-dimensional case; it
can be extended to higher dimensions). Israel junction conditions, then, are
where 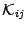 and
and 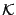 are, respectively, the extrinsic
curvature tensor and its trace and
are, respectively, the extrinsic
curvature tensor and its trace and 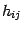 is the induced metric
on
is the induced metric
on 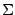 . Here we introduced the standard notation
. Here we introduced the standard notation
![$[A] = \lim_{\eta\rightarrow0^+} \{A(\eta) - A(-\eta)\}$](img16.gif) .
Israel junction conditions describe how the
.
Israel junction conditions describe how the
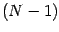 -brane is embedded in the (in principle different) geometries of the
two spacetime domains that it separates.
For our purposes, we are going to write down these equations for a spherical
brane with surface stress energy tensor
-brane is embedded in the (in principle different) geometries of the
two spacetime domains that it separates.
For our purposes, we are going to write down these equations for a spherical
brane with surface stress energy tensor
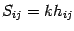 separating two de Sitter spacetimes.
This can be done explicitly
in terms of the radius
separating two de Sitter spacetimes.
This can be done explicitly
in terms of the radius 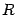 of the brane6.
Then Israel junction conditions reduce to the single differential equation
of the brane6.
Then Israel junction conditions reduce to the single differential equation
![\begin{displaymath}
{\cal H}(R,\dot{R})=\left[ \epsilon \sqrt{\dot{R}^2 + f(R)}
\right]R^{(N-3)} - kR^{N-2} = 0
;
\end{displaymath}](img21.gif) |
(1) |
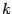 is the constant tension of the brane,
is the constant tension of the brane, 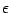 are
signs to be determined by the equation itself [5], and
are
signs to be determined by the equation itself [5], and
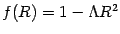 is the metric function appearing in the static line element adapted to the
spherical symmetry for the (anti-)de Sitter spacetime7.
For suitable values of the cosmological constants
equation (1) has two types of solutions: the first is
is the metric function appearing in the static line element adapted to the
spherical symmetry for the (anti-)de Sitter spacetime7.
For suitable values of the cosmological constants
equation (1) has two types of solutions: the first is 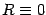 ,
while the second represents a brane collapsing and re-expanding from and
to infinity. For our purpose it is also important to note that
equation (1) can also be obtained by an effective action,
which in the
,
while the second represents a brane collapsing and re-expanding from and
to infinity. For our purpose it is also important to note that
equation (1) can also be obtained by an effective action,
which in the 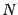 -dimensional case can be written as
-dimensional case can be written as
![\begin{displaymath}
S_{\mathrm{eff.}} =\int \left\{ R^{N-3} \dot{R} \left[ \chi ...
...f(R)}} \right) \right] - {\cal H}(R,\dot{R})
\right \}
d\tau
,
\end{displaymath}](img28.gif) |
(2) |
with the additional constraint 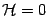 that has to be imposed on the solutions
of the corresponding Euler-Lagrange equation [5].
that has to be imposed on the solutions
of the corresponding Euler-Lagrange equation [5].


Next: 3 Tunnelling
Up: Vacuum decay by p-branes
Previous: 1 Introduction
Stefano Ansoldi
![]() (the
(the ![]() -brane we mentioned above)
can be written in the form
-brane we mentioned above)
can be written in the form
![]() ,
where
,
where ![]() is a Dirac delta, and
is a Dirac delta, and ![]() can be thought as
a transverse coordinate to
can be thought as
a transverse coordinate to ![]() .
In
.
In ![]() -dimensional General Relativity it is possible to write down
the equations of motion for this infinitesimally thin distribution of
matter by splitting Einstein equations in the tangential and
transverse part (see [4] for the
-dimensional General Relativity it is possible to write down
the equations of motion for this infinitesimally thin distribution of
matter by splitting Einstein equations in the tangential and
transverse part (see [4] for the ![]() -dimensional case; it
can be extended to higher dimensions). Israel junction conditions, then, are
-dimensional case; it
can be extended to higher dimensions). Israel junction conditions, then, are