- ... production1
- To
appear in the Proceedings of the 6th International Symposium
on Frontiers in Fundamental and Computational Physics (FFP6),
September 26-29, Udine, ITALY
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sindoni2
- potenzo17@yahoo.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Ansoldi3
- Email: ansoldi@trieste.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... S. Ansoldi3 4
- Webpage: http://www-dft.ts.infn.it/
 ansoldi
ansoldi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... brane5
- In the mathematical
treatment of the classical situation the brane has, in fact, zero radius; from
the physical point of view, with quantum gravity in mind, we can imagine this
brane as a result of zero point quantum fluctuations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... brane6
- We are going to consider
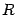 as a function
as a function 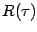 of the proper time
of the proper time 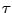 of an observer sitting on the
brane and denote by an overdot the derivative with respect to
of an observer sitting on the
brane and denote by an overdot the derivative with respect to 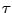 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... spacetime7
- Since the compact
notation could be misleading, we remember that we have two spacetimes with different
cosmological constants
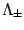 and, thus, two metric functions
and, thus, two metric functions 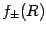 ;
please, also remember the meaning of the square brackets defined above.
;
please, also remember the meaning of the square brackets defined above.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.