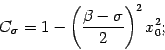

Next: 4 Conclusions
Up: Vacuum decay by p-branes
Previous: 2 Classical Dynamics
The action (2) is crucial in our semiclassical quantization
program, since it can be used to quantize the system via a path integral
approach. Here we are going to consider the tunnelling
process from the 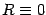 solution to the bounce solution, within the
saddle-point approximation. This gives the possibility to estimate the
following approximated amplitude
solution to the bounce solution, within the
saddle-point approximation. This gives the possibility to estimate the
following approximated amplitude
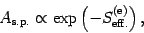 |
(3) |
where
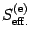 is the Euclidean effective action obtained by
analytically continuing the action (2) to the
Euclidean sector. In order to simplify some expressions, we introduce
the following adimensional quantities:
is the Euclidean effective action obtained by
analytically continuing the action (2) to the
Euclidean sector. In order to simplify some expressions, we introduce
the following adimensional quantities:
Moreover it is a well known result that the adimensional version of the
equation of motion (1) can be cast in the following form
where the prime now denotes the derivative with respect the adimensional time 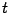 .
The potential
.
The potential 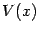 is given by
is given by
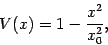 |
(4) |
where
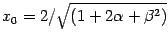 is the adimensional turning radius,
provided that the argument of the square root is positive.
If this condition holds, there is a bounce trajectory, otherwise we have only
the
is the adimensional turning radius,
provided that the argument of the square root is positive.
If this condition holds, there is a bounce trajectory, otherwise we have only
the 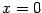 solution. Starting from (2), (3) and
(4) it is possible to evaluate the Euclidean action on the
tunnelling trajectory, i.e on the segment
solution. Starting from (2), (3) and
(4) it is possible to evaluate the Euclidean action on the
tunnelling trajectory, i.e on the segment ![$[0,x _{0}]$](img39.gif) . The final result can
be expressed as
. The final result can
be expressed as
![\begin{displaymath}
S^{(\mathrm{e})}_{\mathrm{eff}}=\frac{x_0 ^{(N-3)/2}}{2(N-2)k^{(N-2)}} \left[
(\beta-\epsilon) J(N,C_{\sigma}) \right],
\end{displaymath}](img40.gif) |
(5) |
where 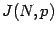 is a function of the dimension of spacetime,
is a function of the dimension of spacetime, 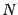 , and of
, and of
with
A detailed description of the functional form of 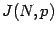 is beyond the
scope of this contribution and can be found elsewhere [7].
We just remark one important feature of it, namely that
is beyond the
scope of this contribution and can be found elsewhere [7].
We just remark one important feature of it, namely that 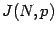 is defined
only when
is defined
only when 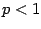 , a condition that, according to the form of
, a condition that, according to the form of 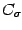 ,
is always satisfied in our case.
,
is always satisfied in our case.


Next: 4 Conclusions
Up: Vacuum decay by p-branes
Previous: 2 Classical Dynamics
Stefano Ansoldi
![]() solution to the bounce solution, within the
saddle-point approximation. This gives the possibility to estimate the
following approximated amplitude
solution to the bounce solution, within the
saddle-point approximation. This gives the possibility to estimate the
following approximated amplitude
![\begin{displaymath}
S^{(\mathrm{e})}_{\mathrm{eff}}=\frac{x_0 ^{(N-3)/2}}{2(N-2)k^{(N-2)}} \left[
(\beta-\epsilon) J(N,C_{\sigma}) \right],
\end{displaymath}](img40.gif)