...S.Ansoldi¹

E-mail address: ansoldi@trieste.infn.it

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...A.Aurilia²

E-mail address: aaurilia@csupomona.edu

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...E.Spallucci³

E-mail address: spallucci@trieste.infn.it

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... rate⁴

At least the first acoustic peak in the power spectrum of temperature fluctuations of the cosmic microwave background, as determined by the Maxima and Boomerang observations, is best fit with 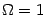$\Omega=1$ as required by inflation.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... scenario⁵

Those revolutionary cosmological data were not available in 1991 when the authors first suggested the possibility that the cosmological constant and dark matter might be related [6]. This paper is based upon an essay (unpublished)that was awarded Honorable Mention in the 1991 Gravity Research Foundation competition.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... time⁶

In the following, by ``boundary'' of an object (point-like or spatially extended) we mean an extremal configuration (initial or final) of the world-history of the object at a finite time, or, in other words, an extremal spacelike section of the object's trajectory in spacetime. The case of an object with a boundary that is spatially open can be treated along similar lines [8] [9].

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... violated⁷

A physical example of such a situation is the emission of an alpha-particle by a radioactive nucleus. Due to quantum tunnelling, the particle suddenly disappears from within the nucleus (its worldline comes to an end point) and reappears at a different point outside the parent nucleus. No physical trajectory connects the two branches of the particle world line. Thus, from the point of view of an external observer, the 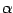$\alpha$-particle world line is semi-infinite: it originates from a point outside the nucleus at a given instant of time and then evolves independently of the parent nucleus.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... bosonization⁸

Introducing fermionic degrees of freedom enables one to establish a correspondence between bosonic and fermionic variables, that is, $J^{\mu\nu\rho}\leftrightarrow \epsilon^{\mu\nu\rho\sigma} \bar\psi \gamma^5 \gamma_\sigma \psi$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

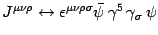... techniques⁹

It seems to us that this result may well be a consequence of a duality between membranes as solitonic solutions of an underlying field theory and membranes as fundamental objects (for a comprehensive review, see Ref. [19]).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... time¹⁰

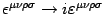$\epsilon^{\mu\nu\rho\sigma} \rightarrow i\varepsilon^{\mu\nu\rho\sigma}$ under Wick rotation. Thus,

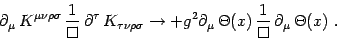$$\partial_\mu K^ {\mu\nu\rho\sigma} {1\over\Box} \par... ...rtial_\mu \Theta(x) {1\over\Box} \partial_\mu \Theta(x) .$$ (50)

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... bubble¹¹

The evolution of the bubble, which is controlled by the two cosmological constants and by the surface tension, can be simulated by the one-dimensional motion of a fictitious particle in a potential [11]; furthermore, a well defined algorithm exists that is capable of determining all possible types of solutions, including inflationary ones, together with the region in parameter space where families of solutions can exist [13]

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.