

Next: C..3 Result for the
Up: C. Explicit computation of
Previous: C..1 Infrared limit
C..2 Ultraviolet limit
To tackle the problem of the ultraviolet behavior of the energy
density, we analyze the limit in which 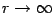 ,
,
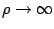 . As already discussed we will first set
. As already discussed we will first set
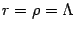 and then approximate the various quantities as
and then approximate the various quantities as
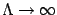 . For the relevant expressions, already encountered above, we
get6
. For the relevant expressions, already encountered above, we
get6
Moreover we also have the well known expansions
which we are going to use in the following. In particular we can
consider in generality the expansion of the following expression
so that
![\begin{displaymath}
- \frac{w ^{3/2}}{2} \ln \left( \frac{z - w ^{1/2}}{z + w ^...
...^{0 , \infty} \frac{w ^{n}}{(2 n
+ 1) z ^{2 n + 1}} \right] .
\end{displaymath}](img312.gif) |
(55) |
From the above result, if we identify
and we consider an overall 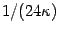 factor, using
properly (50) and the first equation
of (51), we get
factor, using
properly (50) and the first equation
of (51), we get
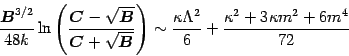 |
(56) |
for the second term in (38). In the same way, starting
again from result (55), together with the
identifications
and taking into account an overall
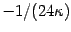 , (49)
and (51), we obtain for the third term
in (38)
, (49)
and (51), we obtain for the third term
in (38)
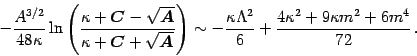 |
(57) |
The last term in (38) has also a logarithmic part and,
using (52), can be approximated as
We are now concerned with the easiest term in (38),
namely the first, for which we get
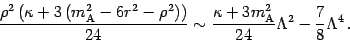 |
(59) |
Summing up equations (56),
(57), (58), (59), we
obtain
| |
|
![$\displaystyle \Lambda ^{4} \left [ 2 \ln \Lambda + \ln 2 - \frac{7}{8}
\right ]...
...ppa + 2 m _{\mathrm{A}} ^{2}}{4} \left( 2 \ln
\Lambda + \ln 2 \right) \right] +$](img327.gif) |
(60) |
| |
|
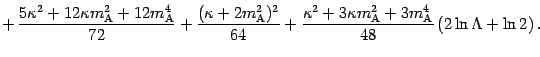 |
|


Next: C..3 Result for the
Up: C. Explicit computation of
Previous: C..1 Infrared limit
Stefano Ansoldi
![]() ,
,
![]() . As already discussed we will first set
. As already discussed we will first set
![]() and then approximate the various quantities as
and then approximate the various quantities as
![]() . For the relevant expressions, already encountered above, we
get6
. For the relevant expressions, already encountered above, we
get6
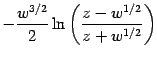

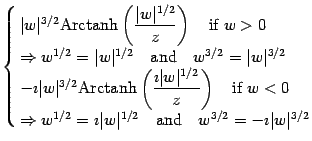
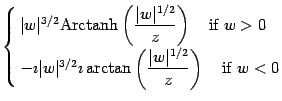
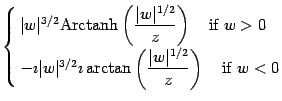
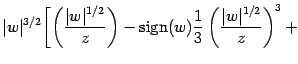
![$\displaystyle \hphantom{\vert w\vert ^{3/2} \Biggl [}
+ \frac{1}{5} \left( \fra...
...sign}} (w) \left( \frac{\vert w\vert ^{1/2}}{z} \right) ^{7} +
\cdots \Biggr] ,$](img311.gif)