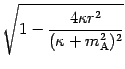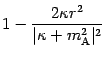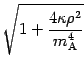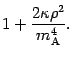

Next: C..2 Ultraviolet limit
Up: C. Explicit computation of
Previous: C. Explicit computation of
C..1 Infrared limit
=1 In this subsection we consider the infrared limit and in the following
we will use the symbol ``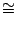 '' to imply that two expression are
equivalent in the infrared limit, i.e. they have the same
limit. Moreover we will get rid of the square roots by means of the
following results
'' to imply that two expression are
equivalent in the infrared limit, i.e. they have the same
limit. Moreover we will get rid of the square roots by means of the
following results
We now turn to the contributions in the various lines of
equation (38). The first one gives no problem:
![\begin{displaymath}
\frac { \rho ^{2} \left[ \kappa + 3 ( m _{\mathrm{A}} ^{2} - 6 r ^{2}
- \rho ^{2} ) \right] } {24} \cong 0 \,.
\end{displaymath}](img262.gif) |
(41) |
The second one has a well behavior in the
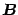 term; more care has
to be paid in the logarithm:
term; more care has
to be paid in the logarithm:
The last term on the second line of (38) again gives
troubles only inside the logarithmic term, which can be elaborated as
follows
Since we also have
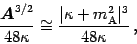 |
(44) |
the two previous results, (44)
and (43), combine in a neat way: the sign in the
first factor exactly combines with the absolute value of the second
factor
so that
For the last term in (38) we do not have too much work.
The factor before the logarithm has no problems and we can simply
forget about the 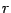 and
and 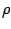 dependent parts. Instead inside the
logarithm we can neglect higher order terms in the limit we are
interested in, so that
dependent parts. Instead inside the
logarithm we can neglect higher order terms in the limit we are
interested in, so that
| |
|
![$\displaystyle \frac{ \left[ \kappa ^{2} + 3 \kappa (m _{\mathrm{A}} ^{2} - 2
r ...
...\right] } {48} \ln
\left( - \kappa \rho ^{2} + \mbox{\boldmath$D$}\right) \cong$](img281.gif) |
|
| |
|
![$\displaystyle \qquad \cong \frac{ \kappa ^{2} + 3 \kappa m _{\mathrm{A}} ^{2} +...
...eft[ - m _{\mathrm{A}} ^{2} ( r ^{2}
+ \rho ^{2} ) - \kappa \rho ^{2} \right] .$](img282.gif) |
(46) |
The desired result,
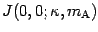 is then
(41)
is then
(41) 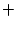 (42)
(42)  (45)
(45)
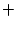 (46), i.e.
(46), i.e.
As also pointed out in the main text this contribution is
finite in the case of vanishing external field (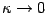 ), since
), since
![\begin{displaymath}
\lim _{\kappa \to 0} \left [ \frac{( \kappa + m _{\mathrm{A...
...athrm{A}}}{24} \left[ \ln (m ^{6} _{\mathrm{A}}) + 1
\right].
\end{displaymath}](img291.gif) |
(48) |


Next: C..2 Ultraviolet limit
Up: C. Explicit computation of
Previous: C. Explicit computation of
Stefano Ansoldi
![]() '' to imply that two expression are
equivalent in the infrared limit, i.e. they have the same
limit. Moreover we will get rid of the square roots by means of the
following results
'' to imply that two expression are
equivalent in the infrared limit, i.e. they have the same
limit. Moreover we will get rid of the square roots by means of the
following results