4 Numerical evaluation of the classical action

As already anticipated in (12) we will evaluate the classical action as the integral of the classical momentum along a classically allowed trajectory. In our case, remembering the naming conventions about the zeros of $\bar{V} (x)$, this implies that the relevant turning points for the bounded trajectory in rescaled coordinates are $R _{1} / H \equiv x _{1} = 0$ and $R _{2} / H \equiv x _{2} = x _{\mathrm{min}}$, so that

$$\bar{S} = \frac{S}{H ^{2}} = 2 \int _{0} ^{x _{\mathrm{min}}} \bar{P} (x) \mathrm{d} x$$

$$= - 2 \int _{0} ^{x _{\mathrm{min}}} x \tanh ^{-1} \left\{ \left( \... ...) \left( x - \vert \Theta \vert \right) ^{2} \right\} } \right\} \mathrm{d} x .$$

The above integral has to be computed when the turning point $x _{\mathrm{min}}$ actually exists, i.e. in the range for $\Theta$ specified by (23). This means that the $\mathrm{Sign}$ at the exponent is always $+1$, and we can forget about it, so that the above turns into

$$\bar{S} = 2 \int _{0} ^{x _{\mathrm{min}}} \bar{P} (x) \... ... ^{3} - 2 x + 2 \vert \Theta \vert} \right\} \mathrm{d} x .$$ (24)

We note that when $x = \Theta$, i.e. the shell is crossing a (double) zero of the external extremal Reißner-Nordström spacetime, the momentum is ill defined, since the argument of the inverse hyperbolic tangent is $-1$. $x = \Theta$ is thus a singularity on the integration path, but, being of the logarithmic type, it is integrable (the leading contribution to the singularity is determined in D).

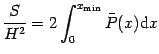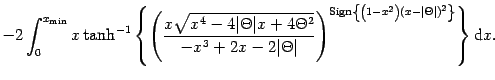The integral in (24) is not exactly computable analytically, but being reassured by the considerations above about its existence, the integration can be performed numerically. We have performed this kind of analysis with Mathematica$^{\circledR}$, evaluating the integral numerically for $10000$ equally spaced test values of $\Theta$ in the interval $[ 10 ^{-4} , (3/4) ^{3/2}]$ and for other $10000$ test values in the interval $[ 10 ^{-16} , 10 ^{-4} ]$ taken as a sequence converging to $0 ^{+}$ as $1 / n ^{4}$ for $n \to + \infty$. 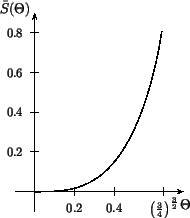The final result is plotted in figure 9.

Figure 9: Graph of the functional dependence of the action from the $\Theta$ parameter as results from the numerical integration of (24) for $20000$ test values of $\Theta$ in the interval $[ 10 ^{-16} , (3/4) ^{3/2}]$ chosen as described in the text.