Dai lavori originali di Bekenstein ed Hawking risulta una sorprendente analogia
tra la dinamica di buchi neri accoppiati a campi di materia quantistici, e
fluidi classici. Tale analogia e` sintetizzata nella cosiddetta ``prima legge'', i.e.
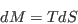 |
(1) |
Dove la massa 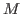 del buco nero funge da energia interna del sistema termodinamico equivalente,
la gravità di superficie determina la temperatura
del buco nero funge da energia interna del sistema termodinamico equivalente,
la gravità di superficie determina la temperatura 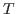 e l'area dell' orizzonte fissa l'entropia
e l'area dell' orizzonte fissa l'entropia
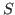 . Si nota subito come l'analogia con i principi della termodinamica classica non sia completa, in quanto
mancano quantità importanti come la pressione ed il volume. Mentre il volume può, intuitivamente,
essere identificato con quello racchiuso dall'orizzonte, quale sia la grandezza geometrica corrispondente alla
pressione è meno chiaro. Nel caso di buchi neri in una geometria di anti-deSitter il candidato
naturale a svolgere il ruolo di pressione è la costante cosmologica.
. Si nota subito come l'analogia con i principi della termodinamica classica non sia completa, in quanto
mancano quantità importanti come la pressione ed il volume. Mentre il volume può, intuitivamente,
essere identificato con quello racchiuso dall'orizzonte, quale sia la grandezza geometrica corrispondente alla
pressione è meno chiaro. Nel caso di buchi neri in una geometria di anti-deSitter il candidato
naturale a svolgere il ruolo di pressione è la costante cosmologica.
In questo scenario abbiamo considerato le fasi termodinamiche, ed in particolare la transizione
di Hawking-Page, per buchi neri sia carichi eletricamente, sia neutri. La transizione di Hawking-Page
ha un ruolo particolarmente importante, in quanto rappresenta la descrizione duale della transizione
di de-confinamento, nell'ambito della dualità tra gravità in 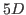 e teorie di gauge in
e teorie di gauge in 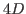 .
.
In particolare, abbiamo
ricavato l' equazione di stato, studiato il regime critico, e mostrato come la costruzione di
Maxwell consente di eliminare una fase a calore specifico negativo, difficilmente giustificabile
fisicamente.
Euro Spallucci
2016-05-19