- ... 1
- E-mail address: ansoldi@trieste.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Castro2
- E-mail address: castro@ctsps.cau.edu
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...E.Spallucci3
- E-mail address: spallucci@vstst0.ts.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
understood4
- There are many interesting reviews on this problem,
as [1], [2], [3], ...and
we apologize for omitting many other good ones.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... respectively5
- The metric signature is
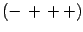 and
in our notation matrices are denoted by boldface letters.
and
in our notation matrices are denoted by boldface letters.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field6
- For the sake of
clarity, let us summarize the canonical dimensions in natural units of
various quantities:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
surface7
- We have assumed that
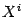 are three spacelike coordinates. By
relaxing this assumptions we can give (38) a slightly different
physical interpretation. If all three
are three spacelike coordinates. By
relaxing this assumptions we can give (38) a slightly different
physical interpretation. If all three 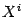 are considered as
transverse directions,
then (38) can be seen as the light-cone gauge
action for a bosonic brane in a
are considered as
transverse directions,
then (38) can be seen as the light-cone gauge
action for a bosonic brane in a 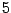 -dimensional target spacetime.
-dimensional target spacetime.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.