When probed at low energy (resolution) an extended object effectively
looks like a point-particle. In this case,
``low energy'' means an energy which is small compared with the energy
scale determined by the brane tension. In natural units, the
tension of a ![]() -brane
has dimension:
-brane
has dimension:
![]() . Thus, when probing the brane at energy
. Thus, when probing the brane at energy
![]() one cannot resolve the extended structure of the object. From this
perspective, the ``point-like limit'' of a
one cannot resolve the extended structure of the object. From this
perspective, the ``point-like limit'' of a ![]() -brane is
equivalent to the ``infinite tension limit''. In either
case, no
higher vibration modes are excited and one expects the brane
to appear concentrated, or ``collapsed'', in its own center of
mass. This critical
limit can be obtained from the general result
(78) by setting
-brane is
equivalent to the ``infinite tension limit''. In either
case, no
higher vibration modes are excited and one expects the brane
to appear concentrated, or ``collapsed'', in its own center of
mass. This critical
limit can be obtained from the general result
(78) by setting
![]() and performing the limit
and performing the limit ![]() using the familiar
representation of the Dirac-delta distribution:
using the familiar
representation of the Dirac-delta distribution:
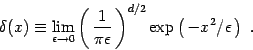 |
(85) |