Quantum strings, or more generally branes of various kind, are currently viewed as the fundamental constituents of everything: not only every matter particle or gauge boson must be derived from the string vibration spectrum, but spacetime itself is built out of them.
If spacetime is no longer preassigned, then logical
consistency demands that a matrix representation of ![]() -brane
dynamics cannot be formulated in any given background
spacetime. The exact mechanism by which
-brane
dynamics cannot be formulated in any given background
spacetime. The exact mechanism by which ![]() -Theory is supposed
to break this circularity is not known at present, but ``loop
quantum mechanics'' points to a possible resolution of that
paradox. If one wishes to discuss quantum strings on the same
footing with point-particles and other
-Theory is supposed
to break this circularity is not known at present, but ``loop
quantum mechanics'' points to a possible resolution of that
paradox. If one wishes to discuss quantum strings on the same
footing with point-particles and other ![]() -branes, then their
dynamics is best formulated in loop space rather than in
physical spacetime. As we have repeatedly stated throughout
this paper, our emphasis on string shapes rather than
on the string constituent points, represents a departure from
the canonical formulation and requires an appropriate choice
of dynamical variables, namely the string configuration
tensor and the areal time. Then, at the loop space level,
where each ``point'' is representative of a particular loop
configuration, our formulation is purely quantum mechanical,
and there is no reference to the background spacetime. At the
same time, the functional approach leads to a precise
interpretation of the fuzziness of the underlying quantum
spacetime in the following sense: when the resolution of the
detecting apparatus is smaller than a particle DeBroglie
wavelength, then the particle quantum trajectory behaves as a
fractal curve of Hausdorff dimension
-branes, then their
dynamics is best formulated in loop space rather than in
physical spacetime. As we have repeatedly stated throughout
this paper, our emphasis on string shapes rather than
on the string constituent points, represents a departure from
the canonical formulation and requires an appropriate choice
of dynamical variables, namely the string configuration
tensor and the areal time. Then, at the loop space level,
where each ``point'' is representative of a particular loop
configuration, our formulation is purely quantum mechanical,
and there is no reference to the background spacetime. At the
same time, the functional approach leads to a precise
interpretation of the fuzziness of the underlying quantum
spacetime in the following sense: when the resolution of the
detecting apparatus is smaller than a particle DeBroglie
wavelength, then the particle quantum trajectory behaves as a
fractal curve of Hausdorff dimension ![]() . Similarly we have
concluded on the basis of the ``shape uncertainty principle''
that the Hausdorff dimension of a quantum string world-sheet
is
. Similarly we have
concluded on the basis of the ``shape uncertainty principle''
that the Hausdorff dimension of a quantum string world-sheet
is ![]() , and that two distinct phases (smooth and fractal
phase) exist above and below the loop DeBroglie area. Now,
if particle world-lines and string world-sheets behave as
fractal objects at small scales of distance, so does the
world-history of a generic
, and that two distinct phases (smooth and fractal
phase) exist above and below the loop DeBroglie area. Now,
if particle world-lines and string world-sheets behave as
fractal objects at small scales of distance, so does the
world-history of a generic ![]() -brane including spacetime
itself [19], and we are led to the general expectation
that a new kind of fractal geometry may provide an
effective dynamical arena for physical phenomena near the
string or Planck scale in the same way that a smooth
Riemannian geometry provides an effective dynamical arena for
physical phenomena at large distance scales.
-brane including spacetime
itself [19], and we are led to the general expectation
that a new kind of fractal geometry may provide an
effective dynamical arena for physical phenomena near the
string or Planck scale in the same way that a smooth
Riemannian geometry provides an effective dynamical arena for
physical phenomena at large distance scales.
Once committed to that point of view, one may naturally ask,
``what kind of physical mechanism can be invoked in the
framework of loop quantum mechanics to account for the
transition from the fractal to the smooth geometric phase of
spacetime?''. A possible answer consists in the phenomenon of
![]() -brane condensation. In order to illustrate its
meaning, let us focus, once again, on string loops. Then, we
suggest that what we call ``classical spacetime'' emerges as a
condensate, or string vacuum similar to the ground state of a
superconductor. The large scale properties of such a state
are described by an ``effective Riemannian geometry''. At a
distance scale of order
-brane condensation. In order to illustrate its
meaning, let us focus, once again, on string loops. Then, we
suggest that what we call ``classical spacetime'' emerges as a
condensate, or string vacuum similar to the ground state of a
superconductor. The large scale properties of such a state
are described by an ``effective Riemannian geometry''. At a
distance scale of order
![]() , the condensate
``evaporates'', and with it, the very notion of Riemannian
spacetime. What is left behind, is the fuzzy stuff of quantum
spacetime.
, the condensate
``evaporates'', and with it, the very notion of Riemannian
spacetime. What is left behind, is the fuzzy stuff of quantum
spacetime.
Clearly, the above scenario is rooted in the functional
quantum mechanics of string loops discussed in the previous
sections, but is best understood in terms of a model which
mimics the Ginzburg-Landau theory of superconductivity. Let
us recall once again that one of the main results of the functional
approach to quantum strings is that it is possible to describe
the evolution of the system without giving up
reparametrization invariance. In that approach,
the clock that times the evolution of a closed bosonic string
is the internal area,
i.e., the area measured in the string parameter space
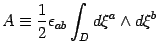 ,
of any surface subtended by the string loop. The choice of
such a surface is arbitrary, corresponding to the freedom of choosing the
initial instant of time, i.e., a fiducial reference area.
Then one can take advantage of this arbitrariness in
the following way. In particle field theory an arbitrary lapse of Euclidean,
or Wick rotated, imaginary time between initial and final
field configurations is usually given
the meaning of inverse temperature
,
of any surface subtended by the string loop. The choice of
such a surface is arbitrary, corresponding to the freedom of choosing the
initial instant of time, i.e., a fiducial reference area.
Then one can take advantage of this arbitrariness in
the following way. In particle field theory an arbitrary lapse of Euclidean,
or Wick rotated, imaginary time between initial and final
field configurations is usually given
the meaning of inverse temperature
| (47) |
Following the same procedure, we suggest to analytically
extend ![]() to imaginary values,
to imaginary values,
![]() , on the assumption that the resulting
finite area loop quantum mechanics will provide a
statistical description of the string vacuum
fluctuations. This leads us to consider the following
effective (Euclidean) lagrangian of the Ginzburg-Landau type,
, on the assumption that the resulting
finite area loop quantum mechanics will provide a
statistical description of the string vacuum
fluctuations. This leads us to consider the following
effective (Euclidean) lagrangian of the Ginzburg-Landau type,
| (50) |