2 Fluctuations of the gravitational energy density

We will now consider a single quantum fluctuation of the vacuum energy density and assume that it is uniformly spread over a spherical region³ - a ``bubble''; then we find that the total energy associated with the fluctuation is

$$E=\frac{4\pi }{3}R_{0}^{3}\rho ,$$

where $R_{0}$ is the radius of the bubble. Of course it is not obvious at all that fluctuations of arbitrary total energy may be observed: one expects that nonlinear effects should affect the formation of a fluctuation and only a complete theory of quantum gravity would be the correct framework to understand the process in full detail⁴. Here we neglect these important details, we only require that the total energy of the fluctuation satisfies the time-energy uncertainty principle. This means that a fluctuation with total energy $E$ has a duration $\Delta t$ given by

$$\Delta t \approx \frac{\hbar}{E} = \frac{3 \hbar }{4 \pi R _{0} ^{3} \rho } .$$ (1)

The observer who detects the fluctuation may still observe it if the energy density keeps decreasing so that the uncertainty principle is satisfied at all times (this is not possible for other quantum fluctuations, like those of the electronic field, which have a nonzero lower bound for the total energy). Moreover the observer may communicate with observers who are further away from the apparent centre of the fluctuation and these observers may in turn ``see'' the fluctuation (the network of observers acts as a single composite detector); thus a fluctuation appears to expand at the speed of light, the highest speed at which the information that the fluctuation has been observed may propagate. We wish to remark that this point of view is not new and that the informational approach to problems in General Relativity has been pioneered many years ago by H. Bondi [9], who introduced the so-called news function to relate the emission of gravitational waves with mass changes of gravitating systems. The expansion of the bubble may then be viewed as the spread of information from a system with changing energy density and in turn this spread can be related to a kinetic/radiative component associated with the processes of bubble formation and evolution. In other words we assume that the perturbation is a sort of spherically symmetric gravitational wave - allowed by energy nonconservation in the fluctuation - that expands outwards with the speed of light. If we adhere to this point of view then, as the bubble appears to spread in space, no observer at distance $r$ from the point in which the fluctuation occurs can infer the existence of the bubble before a time $r/c$. As soon as an observer becomes aware of the fluctuation, he may also measure its size $R_{0}$: since the bubble boundary appears to expand at the speed of light, we can correlate the radius $% R_{0}$ of the bubble with its lifetime $\Delta t$: $R_{0}=c\Delta t$. Moreover 1 must hold at all times, and therefore we find

$$\rho \approx \frac{3 \hbar c}{4 \pi R _{0} ^{4}} = \frac{3 \hbar}{4 \pi c ^{3} \Delta t ^{4}} .$$

Now let $n ({\vec{x}} , t)$ be the number density of the fluctuations which occur in spacetime, i.e., $n({\vec{x}},t) \mathrm{d} V \mathrm{d} t$ fluctuations are created in a small space-time volume $\mathrm{d} V \mathrm{d} t$ at position ${\vec{x}}$ and time $t$, and assume that $n({\vec{x}},t) \mathrm{d} V \mathrm{d} t$ is a Poisson variate with average $n_{0} \mathrm{d} V \mathrm{d} t$ (so that the variance equals $n_{0} \mathrm{d} V \mathrm{d} t$ as well)⁵. Then the average energy density at a given observation point ${\vec{x}_{0}}$ due to the fluctuations created at distance $r$ at an earlier time $t^{\prime}$ is

$$\mathrm{d} ^{2}\rho ={\frac{{3\hbar }}{{4\pi c^{3}(t-t^{\pri... ...rime })^{4}}}} \cdot r^{2}\mathrm{d} r \mathrm{d} t^{\prime }.$$

Of course this contribution is different from zero only if the information that the bubble exists has the time to propagate as far as the observation point ${\vec{x}_{0}}$, i.e., if $c(t-t^{\prime })>r$. Thus the total average energy density at the observation point ${\vec{x}_{0}}$ due to all shells of radius $r$ inside the light cone is

$$\rho _{{\mathrm{tot}}}(t) = \int\limits_{r_{{\mathrm{min}} }... ...{\frac{{3\hbar n_{0} } }{{c^3(t-t^{\prime})^4}}} \cdot r^2}} ,$$

where $T_{0}$ is the age of the Universe. This formula can be simplified noting that the time integral can be approximated without appreciable error by setting $T_{0}\approx \infty$. Obviously this is true only as long as we limit ourselves to a sufficiently old Universe: in the case of a young Universe we would obtain an explicit time dependence of the average energy density, so that the energy density would be a nonstationary random process. Although the stationarity, which is invoked here and in the following sections, is not exact, we shall make this simplifying assumption, so that

$$\rho _{{\mathrm{tot}}}(t) \approx \int\limits_{r_{{\mathrm{min}} }}^{r_{{\mathrm{max}} }} {\mathrm{... ...athrm{d} t^{\prime}{\frac{{3\hbar n_{0} } }{{c^3(t-t^{\prime})^4}}} \cdot r^2}}$$

$$= {\frac{{3\hbar n_{0} } }{{c^3}}} \int\limits_{r_{{\mathrm{min}} }... ...nt_{-\infty }^{t-r/c} {{\frac{{\mathrm{d} t^{\prime}} } {{(t-t^{\prime})^4}}}}}$$

$$= \hbar n_{0} \ln {\frac{{r_{{\mathrm{max}} }} }{{r_{{\mathrm{min}} }}}} .$$ (2)

This equation contains a maximum and a minimum value for the radial coordinate: the maximum distance can be taken to be the radius of the universe $r_{{\mathrm{max}}}=R_{U}$, while the minimum distance cannot be smaller than the Schwarzschild radius for a bubble (if it were smaller, then no observer could know that the bubble exists), so that

$$r_{{\mathrm{min}} }={\frac{{2GM}}{{c^{2}}}}={\frac{2G}{{c^{2... ...\Delta t}}}= {\frac{{2G\hbar }}{ {c^{3}r_{{\mathrm{min}} }}}},$$

i.e.,

$$r_{{\mathrm{min}} }=\sqrt{{\frac{{2G\hbar }}{{c^{3}}}}} = l_{P},$$

which is just the Planck length⁶ $l_{\mathrm{P}}=\sqrt{2G\hbar/c^{3}}$; finally the total energy density turns out to be

$$\rho _{{\mathrm{tot}}}=\hbar n_{0} \ln{\frac{R_{U}}{l_{\math... ... {\frac{{c^{3}R_{U}^{2}}}{{2G\hbar }} \approx 140}\hbar n_{0}.$$ (3)

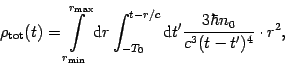
Some comments on the above results are in order: the first one is that at the end the result does not depend on $t$ and obviously it does not depend on the choice of the observation point ${\vec{x}_{0}}$. This is a consequence of the space-time translational invariance of the random process that produces the fluctuations. Moreover, we have neglected some important details, for instance we have implicitly assumed that the total density is just the sum of the densities due to each single fluctuation, which calls for a linearized version of the gravitational field (this is certainly not correct in the vicinity of a large compact mass). However the value of this simple model lies in the ability to calculate such quantities as the average energy density 3. Indeed we can go further and, using the same formalism, we can also compute the variance $\sigma _{\rho }^{2}$ of the energy density, assuming that the only sources of randomness are the uncorrelated Poisson variates $n({\vec{x}},t) \mathrm{d} V \mathrm{d} t$. The contribution to the total variance from all the shells at distance $r$ at an earlier time $t^\prime$ is

$$\mathrm{d} ^{2}\sigma^{2}_{\rho} = \left( {{\frac{{3\hbar } ... ...pi c^6(t-t^{\prime})^8}}}\cdot r^2 \mathrm{d} r \mathrm{d} t ,$$

and therefore the total variance is

$$\sigma _{\rho }^{2} {=} \int\limits_{r_{{\mathrm{min}} }}^{r_{{\mathrm{max}} }} {\mathrm{... ...rime }{\frac{{9\hbar ^{2}n_{0}}}{{4\pi c^{6}(t-t^{\prime })^{8}}}}\cdot r^{2}}}$$

$${=} {\frac{{9\hbar ^{2}n_{0}}}{{4\pi c^{6}}}} \int\limits_{r_{{\mathr... ...-\infty }^{t-r/c}{{\frac{{\mathrm{d} t^{\prime }}} {{(t-t^{\prime })^{8}% }}}}}$$

$${=} {\frac{{9\hbar^{2} cn_{0}}}{{28 \pi}}} \int\limits_{r_{{\mathrm{m... ...\frac{{c^{6}}}{{4G^{2}\hbar ^{2}}}}={\frac{{9c^{7}n_{0}}}{{% 448G^{2} \pi }}} .$$ (4)

It is interesting to note that, unlike the average value 3, the variance 4 is essentially due to the fluctuations in a restricted neighbourhood of the observer, while the other fluctuations just average out and do not contribute significantly. Moreover, since the radius of the Universe changes with time, equations 2 and 4 mean that the energy density is actually only a weakly stationary random process, in the sense that the mean value slowly changes, while the variance remains constant (note that this does not coincide with the usual definition of weak stationarity). One more important comment is that the expanding bubbles are just a representation of the light cones in 3-space, therefore they are Lorentz invariant, i.e., they would look the same in any other Lorentz-boosted reference frame. Thus these fluctuations satisfy the requirement, first discussed by Zeldovich [10], that the quantum vacuum must be Lorentz invariant.

Finally we wish to remark that the average energy density results from the (linear) superposition of non-negative energy densities and therefore the probability density of the energy density fluctuations cannot be a Gaussian density. Moreover some of these fluctuations are exceedingly large (when and where the bubble is very small), so that we expect the variance to be much larger than the average value (a very similar situation holds for the distribution of energy loss in the interaction of charged particles with matter, which leads to the well-known Landau distribution).