- ... 1
- E-mail address: ansoldi@trieste.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Aurilia2
- E-mail address: aaurilia@csupomona.edu
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 3
- E-mail address: spallucci@vstst0.ts.infn.it
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Smailagic4
- E-mail address: anais@etfos.hr
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
undefined5
- Here
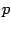 stands for the number of world indices, or rank,
of the gauge potential, and
stands for the number of world indices, or rank,
of the gauge potential, and 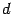 represents the number of spacetime
dimensions. The metric is Minkowskian and our signature convention is
represents the number of spacetime
dimensions. The metric is Minkowskian and our signature convention is
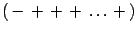 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
empty6
- In a Riemannian spacetime, with non zero curvature,
that arbitrary constant cannot be set, in general, equal to zero, and plays
the physical role of a ``cosmological constant'' [4]. As a matter of
fact, the role of that constant is of paramount importance in most
models of cosmic inflation [5].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... form7
- In the
following discussion we have suppressed all indices in order to simplify the
notation. Thus, the Hodge dual of a
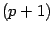 -form, including the appropriate
combinatorial factor, is simply indicated by
-form, including the appropriate
combinatorial factor, is simply indicated by
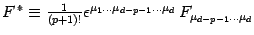 ,
while the product of two
,
while the product of two 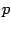 -forms becomes:
-forms becomes:
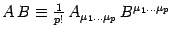 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... zero-form8
- We have chosen the symbol
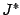 for the zero-form to
order to match the notation in the parent Lagrangian (19). Note that
the same reasoning applies to the `` magnetic '' current
for the zero-form to
order to match the notation in the parent Lagrangian (19). Note that
the same reasoning applies to the `` magnetic '' current 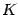 in the absence
of an `` electric '' current
in the absence
of an `` electric '' current 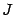 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.