We first note that the quantization can be interpreted as giving a
relation among the parameters of the model, in our case the charge ![]() and the
de Sitter cosmological horizon
and the
de Sitter cosmological horizon ![]() . Let us take for example a total action of the
order of the quantum,
. Let us take for example a total action of the
order of the quantum,
![]() , i.e. associated to a state with
quantum number
, i.e. associated to a state with
quantum number ![]() , for a de Sitter cosmological horizon
, for a de Sitter cosmological horizon ![]() .
Then
.
Then
![]() , i.e.
, i.e.
![]() , so that
, so that
![]() .
This shows, as a preliminary estimate, that a small gravitational system
with quantum properties is conceivable.
.
This shows, as a preliminary estimate, that a small gravitational system
with quantum properties is conceivable.
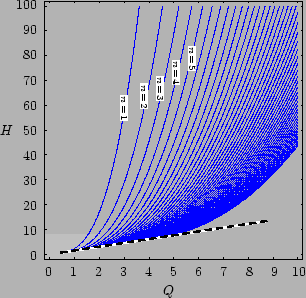
We can also see how the action behaves for variations of the parameters ![]() and
and ![]() by a numerical plot of the level curves of the action. This is shown in figure 10.
by a numerical plot of the level curves of the action. This is shown in figure 10.
 |
||
|
Figure: Graph of the level curves
for the action for the level values
|
||
 |
||
|
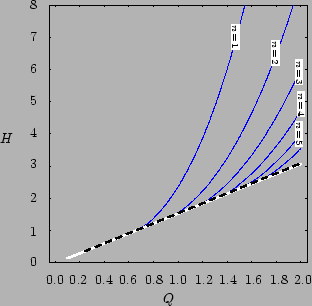
Figure 11: Blow up of the region
of small
|
||