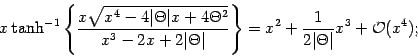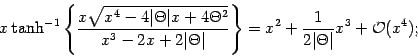

Next: F. Acknowledgments
Up: WKB Metastable States
Previous: D. Character of the
E. Parameter dependence of the Action
We consider the action integral (24). Expanding the integrand
we get
Then the upper integration limit, 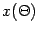 , can be expanded as
, can be expanded as
so that when both expansions hold, we can write
We thus see that the leading term for small 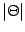 is
is
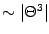 .
.
Stefano Ansoldi