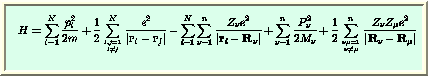
Potenziali quantistici

Tra le tecniche che simulano l'interazione fra i nuclei e gli elettroni con un approccio che segue le leggi della meccanica quantistica c'è il ab initio.

Per poter costruire un algoritmo in grado di risolvere l'equazione che descrive un sistema (avente un certo numero di nuclei ed elettroni) è però quasi sempre necessario fare alcune approssimazioni.

La complicatissima equazione che descrive un sistema a molti corpi chiamata Hamiltoniana.

Queste approssimazioni consentono di arrivare a studiare il problema come se fosse quello di un singolo elettrone che si trova in un potenziale elettrostatico medio (dovuto dalla presenza di tutti gli altri elettroni e dei nuclei) con in più il termine quantistico che tiene conto del fatto che gli elettroni sono particelle identiche.

L'Hamiltoniana per un elettrone.

Dal punto di vista numerico-computazionale, uno dei modi per risolvere l'equazione è quello di fare dei tentativi e di iterare il processo fin tanto che il risultato non va a convergenza, cioè che nei passaggi dell'iterazione ad un certo punto il penultimo iter dà un risultato pressochè identico all'ultimo.