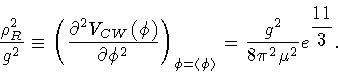

Next: Bibliography
Up: Membrane Vacuum as a
Previous: 4. Dynamics of the
The scenario emerging from the last
section is based on the assumption that the
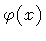 -field can acquire a non vanishing vacuum expectation value.
Note that there is no potential term for
-field can acquire a non vanishing vacuum expectation value.
Note that there is no potential term for
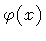 in the
classical action (8). However, we wish to show that a self-consistent
potential may originate from the quantum fluctuations of the
in the
classical action (8). However, we wish to show that a self-consistent
potential may originate from the quantum fluctuations of the
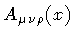 field leading to a non vanishing vacuum
expectation value for the order parameter. On the technical side, this means
to compute the one-loop effective potential for the
field leading to a non vanishing vacuum
expectation value for the order parameter. On the technical side, this means
to compute the one-loop effective potential for the
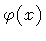 field
by integrating
field
by integrating
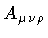 out of the functional integral
out of the functional integral
![\begin{displaymath}Z
=
\int \left[ D \Psi ^{*} [S] \right] \left[ D \Psi [S] \...
...\nu \rho}(x) ]
\exp \left( i {\mathcal{S}} / \hbar \right)
.
\end{displaymath}](img93.gif) |
(31) |
The quantization of higher rank gauge fields is a lengthy procedure
involving a sequence of gauge fixing conditions together with
various generations of ghosts [11]. In principle, these terms
should be included in the functional measure in the action
functional. However, in our case they are unnecessary since we know
already that in the superconducting phase
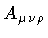 describes
a massive scalar degree of freedom which is the only physical degree of
freedom. Thus, the effective potential is
describes
a massive scalar degree of freedom which is the only physical degree of
freedom. Thus, the effective potential is
The ultraviolet divergences of the one-loop determinant have been
regularized through the cutoff 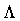 ,
and the two counterterms
,
and the two counterterms
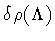 and
and
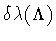 are fixed by the
renormalization conditions
are fixed by the
renormalization conditions
| |
|
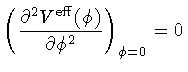 |
(32) |
| |
|
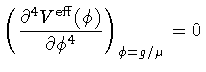 |
(33) |
in which 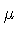 appears as an arbitrary renormalization scale. The scalar field
appears as an arbitrary renormalization scale. The scalar field
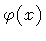 has no classical dynamics of its own, i.e., it possesses
no kinetic or potential term.
This is the reason for imposing the two conditions (32),(33):
equation (32) is the characteristic Coleman-Weinberg condition
[3] ensuring that the mass of the gauge field is non vanishing only
in the condensed phase
has no classical dynamics of its own, i.e., it possesses
no kinetic or potential term.
This is the reason for imposing the two conditions (32),(33):
equation (32) is the characteristic Coleman-Weinberg condition
[3] ensuring that the mass of the gauge field is non vanishing only
in the condensed phase
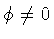 ;
equation (33) follows from the
absence of a classical quartic self-interaction. Of course, the physical
properties of the system are insensitive to the choice of the
renormalization condition. Then, with our choice,
we find the Coleman-Weinberg potential for membranes
;
equation (33) follows from the
absence of a classical quartic self-interaction. Of course, the physical
properties of the system are insensitive to the choice of the
renormalization condition. Then, with our choice,
we find the Coleman-Weinberg potential for membranes
![\begin{displaymath}V _{CW} (\phi)
=
\frac{\phi ^{4}}{64 \pi ^{2}}
\left[
\ln \frac{\phi ^{2} \mu ^{2}}{g ^{2}}
-
\frac{25}{6}
\right]
.
\end{displaymath}](img104.gif) |
(34) |
The absolute minimum of
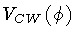 corresponds to a super-conducting phase
characterized by a vacuum expectation value of the order parameter
corresponds to a super-conducting phase
characterized by a vacuum expectation value of the order parameter
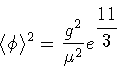 |
(35) |
and by a dynamical surface tension
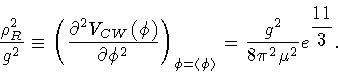 |
(36) |
The factor
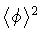 as given by (35) is also
the square of the dynamically generated mass for
as given by (35) is also
the square of the dynamically generated mass for
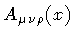 .
Hence, the physical thickness of the membrane, is of the order of
.
Hence, the physical thickness of the membrane, is of the order of
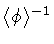 ,
and the dynamically generated surface tension is
,
and the dynamically generated surface tension is
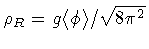 .
This quantity is
positive, so that the bubbles of ordinary vacuum tend to collapse in
the absence of a balancing internal pressure. In the case of
``hadronic bags'', this internal pressure is provided by the
quark-gluon complex. In any event, the picture
of the superconducting membrane vacuum is
strongly reminiscent of the classical dynamics of a closed membrane
coupled to its gauge partner i.e.,
.
This quantity is
positive, so that the bubbles of ordinary vacuum tend to collapse in
the absence of a balancing internal pressure. In the case of
``hadronic bags'', this internal pressure is provided by the
quark-gluon complex. In any event, the picture
of the superconducting membrane vacuum is
strongly reminiscent of the classical dynamics of a closed membrane
coupled to its gauge partner i.e.,
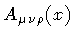 [4]. In both cases, vacuum
bubbles created in one vacuum phase evolve and die in a different
vacuum background. This suggests a new possibility of quantum vacuum
polarization via the creation and annihilation of whole domains of
spacetime in which the energy density is different from that of the
ambient spacetime. As a matter of fact, the
novelty of our field model is the onset of a new type of ``Higgs
mechanism for membranes'' triggered solely by quantum fluctuations.
The effect of such fluctuations can be accounted for by an effective
potential. As in Umezawa's approach, this effective potential is
consistent with the dynamical generation of a bag with surface
tension out of the vacuum.
[4]. In both cases, vacuum
bubbles created in one vacuum phase evolve and die in a different
vacuum background. This suggests a new possibility of quantum vacuum
polarization via the creation and annihilation of whole domains of
spacetime in which the energy density is different from that of the
ambient spacetime. As a matter of fact, the
novelty of our field model is the onset of a new type of ``Higgs
mechanism for membranes'' triggered solely by quantum fluctuations.
The effect of such fluctuations can be accounted for by an effective
potential. As in Umezawa's approach, this effective potential is
consistent with the dynamical generation of a bag with surface
tension out of the vacuum.


Next: Bibliography
Up: Membrane Vacuum as a
Previous: 4. Dynamics of the
Stefano Ansoldi
Department of Theoretical Physics
University of Trieste
TRIESTE - ITALY
![]() -field can acquire a non vanishing vacuum expectation value.
Note that there is no potential term for
-field can acquire a non vanishing vacuum expectation value.
Note that there is no potential term for
![]() in the
classical action (8). However, we wish to show that a self-consistent
potential may originate from the quantum fluctuations of the
in the
classical action (8). However, we wish to show that a self-consistent
potential may originate from the quantum fluctuations of the
![]() field leading to a non vanishing vacuum
expectation value for the order parameter. On the technical side, this means
to compute the one-loop effective potential for the
field leading to a non vanishing vacuum
expectation value for the order parameter. On the technical side, this means
to compute the one-loop effective potential for the
![]() field
by integrating
field
by integrating
![]() out of the functional integral
out of the functional integral
![\begin{displaymath}Z
=
\int \left[ D \Psi ^{*} [S] \right] \left[ D \Psi [S] \...
...\nu \rho}(x) ]
\exp \left( i {\mathcal{S}} / \hbar \right)
.
\end{displaymath}](img93.gif)
![\begin{displaymath}V _{CW} (\phi)
=
\frac{\phi ^{4}}{64 \pi ^{2}}
\left[
\ln \frac{\phi ^{2} \mu ^{2}}{g ^{2}}
-
\frac{25}{6}
\right]
.
\end{displaymath}](img104.gif)