Introduzione alla minimizzazione di funzioni


Il problema di minimizzare (equivalente in modo banale, cambiando il segno,  a massimizzare)  una funzione reale di una o più variabili reali è  estremamente importante in fisica.
Questo estremo interesse in Fisica per metodi di minimizzazione ha anche portato a ibridazioni estremamente fruttuose tra matematica numerica e fisica. In più di un' occasione, nuovi metodi di ottimizzazione sono stati proposti a partire da analogie o sfruttando proprietà dei sistemi fisici.

Una prima distinzione tra problemi di minimo riguarda i problemi di minimo globale  e locale.
Ricordiamo che un punto xmin del dominio D di una funzione si dice punto di minimo assoluto/globale  se

                                                            f(xmin) ≤  f(x)     ∀ x ∈ D     [1]

mentre è un minimo relativo se la disuguaglianza vale solo per un intorno di xmin appartenente a D.

Il problema di determnare in modo efficiente numero e posizione dei punti di minimo globale costituisce uno dei problemi più  complessi dell' analisi numerica ed è tuttora un argomento di ricerca attiva.

Il problema di determinare un minimo relativo (locale) è  invece meglio compreso ed esistono numerosi algoritmi  sufficientemente rodati ed analizzati.

In queste note non toccheremo  gli algoritmi moderni  per la minimizzazione di  funzioni di più variabili (gradienti coniugati, metodi quasi-newton)  ma ci limiteremo a discutere il metodo dello Steepest-Descent, noto per essere altamente inefficiente nel caso di problemi  mal condizionati con  funzioni di più variabili (vedi dopo per la definizione di problema di minimo mal condizionato), e tuttavia, per la sua semplicità, può costituire un punto di partenza  per la soluzione numerica di problemi di bassa dimensionalità. Inoltre permette di discutere in modo semplice l' origine delle difficoltà in più di una dimensione dando  anche la possibilità di  avere una prima idea su cosa possa voler dire un approccio "da fisici" al problema della minimizzzione.

Metodo dello Steepest-Descent a passo fisso

Supponiamo di essere  in grado di calcolare la derivata (o  tutte le derivate parziali, per funzioni di n variabili)  della funzione di cui cerchiamo il minimo,  per tutti i punti del suo dominio.

Iniziamo col caso di funzioni di una variabile.   Se vediamo la funzione da minimizzare come una funzione energia potenziale  u(x),  e la ricerca del minimo come la ricerca del punto di  equilibrio stabile,  la soluzione del problema può  esserci suggerita dal  comportamento di sistemi fisici  con attrito dipendente dalla velocità, in regime di sovrasmorzamento:  la dinamica è ben approssimata da equazioni del moto  del tipo

                                                                    v = w F

dove v è la velocità,  w  una costante positiva e F= -du/dx la forza.  Dove la forza è maggiore lì   il sistema si muove più velocemente, mentre,   dove la forza si annulla abbiamo un punto di equilibrio del sistema. Discretizzando l' equazione differenziale per x(t),   risulta evidente che, secondo   questa "dinamica smorzata"  un punto di minimo del potenziale  corrisponde al  punto fisso della  trasfomazione

                                                x(n+1)  =   x(n)  +   α   F(x(n))                          [2]
 
dipendente dal parametro α.
La teoria  sui punti fissi di trasformazioni  del tipo [2]  ci dice che  in un intorno del punto di equilibrio esisterà  un valore di α > 0 sufficienteente piccolo da  garantire la converenza dell' algoritmo  al punto di minimo.  Inoltre, il valore critico di α al di sopra del quale l' algoritmo cessa di convergere, sarà  tanto più piccolo quanto maggiore la curvatura (la deivata seconda)  del potenziale al minimo.

Caso con n variabili. 
Con una funzione di più  variabili  u(x1,x2,...,xN)  le idee sopra esposte possono essere riutilzzate direttamente per arrivare ad un algoritmo (lo Steepest-Descent a passo fisso)   che è  la generalizzazione diretta della trasformazione [2]:

                        xi(n+1)  =   xi(n)  +   α   Fi(x1(n),x2(n),...,xN(n))                         [3]

L' analisi della trasformazione [3] è  semplificata dall' osservazione che in un intorno del minimo (m1,m2,...,mN)  le "forze"  che appaiono nellla [3] hanno una struttura semplice. Infatti la funzione da minimizzare (potenziale) può  essere  espansa in serie di Taylor di più variabili :

                   u(x1,x2,...,xN) = u(m1,m2,...,mN) + ∑i,jHij(xi-mi) (xj-mij)                   [4]

dove  la matrice    Hij = [(1/2)∂2u/∂xi∂xj ]  è  una matrice simmetrica, definita positiva.  Pertanto diagonalizzabile. Nella base degli autovettori di H, nell' intorno del minimo, le [3] possono essere riscritte come N  equazioni disaccoppiate del tipo [2], per ciascuna delle variabili   xi.

Questa osservazione dà una prima idea di quali possano essere i problemi per cui l' algritmo risulti poco efficiente: basta che un solo autovettore di H corrisponda ad un autovalore molto maggiore degli altri, perché  questo limiti il valore massimo del parametro  α   per tutti i gradi di libertà.

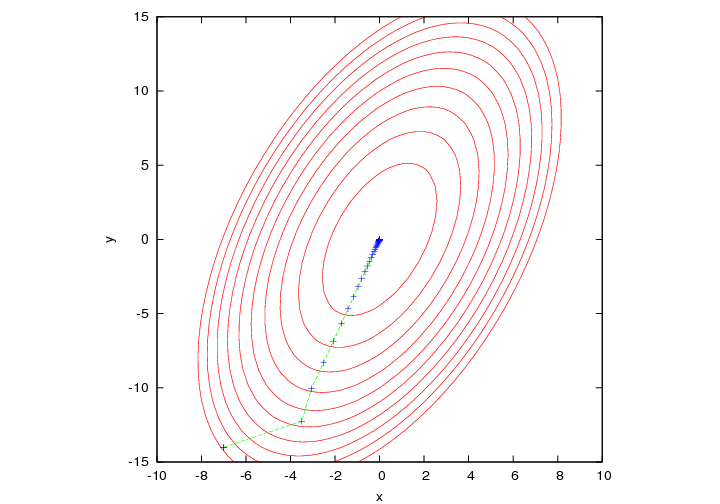
Inoltre, in queste condizioni, corrispondenti ad una buca di potenziale molto asimmetrica attorno al punto di minimo, c'è  un ulteriore limite dell' algoritmo che interviene a renderlo poco efficiente. Illustriamo la situazione in 2D per semplicità  di visualizzazione,  anche se l' argomento è di validità  generale.

Nell' intorno del minimo le curve di livello corrispondenti ad un valore costante del potenziale costituiscono una famiglia di ellissi concentriche al punto di minimo e la cui eccentricità  dipende dal mal condizionamento del problema, quantificato dal numero di condizionamento della matrice H. Ricordiamo che il numero di condizionamento di una matrice diagonalizzabile corrisponde al rapporto tra massimo e minimo autovalore.

Grandi differenze tra gli autovalori (positivi) di H corrispondono ad una "valle" attorno al minimo molto "allungata"  in una direzione.
La trasformazione  [3]  corrisponde a far  muovere il punto rappresentativo del sistema lungo la direzione della forza nel punto di partenza.
Il vettore forza è (a parte il segno) il gradiente della superficie di energia potenziale. Si può far vedere che il gradiente in un punto di una funzione   u(x1,x2,...,xN)  è  sempre ortogonale alla curva di livello che passa per quel punto1. Pertanto la successione delle trasformazioni [3] corrisponde ad una spezzata in cui ogni segmento deve essere ortogonale alla curva di livello su cui termina. Questo, come esemplificato nella figura, può rendere estremamente lenta la convergenza al minimo e quindi dar conto delle difficoltà  del metodo (anche se non apprezzabile sula scala dela figura,   segmenti successivi tendono ad allinearsi con l' asse maggiore delle ellisse ma non conicindono mai con questo).




                                                                                   
                                                                                        Path of steepest descent approximations for the minimum
                                                                                           Le croci evidenziano i punti successivi ottenuti  nella
                                                                                           ricerca del minimo mediante Steepest-Descent a passo
                                                                                           fisso.





1 Una curva di livello è caratterizzata dalla condizione u(x,y) = costante. Il differenziale di questa funzione sarà du=∂u/∂x dx + ∂u/∂y dy = 0.  Questa condizione può essere interpretata come la condizione di ortogonalità tra il vettore gradiente (∂u/∂x , ∂u/∂y) e il vettore tangente alla curva di livello: (dx , dy).