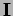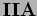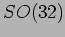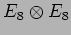Next: About this document ...
Introduzione alla Teoria delle Stringhe
A.A. 2009-10
Introduzione e discussione generale
- 29-09-09:
Presentazione del corso:
motivazioni ed obiettivi; contenuti. Testi di
riferimento e materiale bibliografico on-line.
- 29-09-09:
``Contro-disinformazione'':
Cosa NON è la
Teoria delle Stringhe. Preconcetti ed idee sbagliate.
Ignoranza e malafede.
- 30-10-09 :
Perchè studiare la Teoria della Teoria delle Stringhe.
``Particelle elementari'' come modi vibrazionali della
stringa.``Unificazione'' in Teorie di Stringa. QFTs come
``teorie efficaci'' a bassa energia.
- 30-10-09:
Coordinate
della stringa; Superficie d' universo.; bi-vettore tangente;
l' Azione di Nambu-Goto: significato geometrico.
- 01-10-09:
Limite non-relativistico dell'azione di Nambu-Goto.
Metrica Indotta , e metrica della stringa.
Azione di Nambu-Goto in termini della metrica indotta. Invarianza
per ri-parametrizzazioni.
- 01-10-09:
L' azione di Polyakov:
invarianza di Lorentz come ``simmetria interna''. Equazioni di campo ed equazioni di
Vincolo. Soluzione della metrica di stringa in termini della metrica indotta.
Equivalenza classica tra l'azione di Polyakov e l'azione di Nambu-Goto.
- 06-10-09:
Gauge conforme. Equazioni di vincolo, e variabili
dinamiche indipendenti.Incompatibilità tra Invarianza di Lorentz e
quantizzazione:
il concetto di ``dimensione critica'' dello spaziotempo.
- 06-10-09:
Estensione supersimmetrica dell'azione di Polyakov nella gauge
conforme. Componenti Chirali. Left/right-movers.
- 07-10-09:
Condizioni ai bordi per le coordinate fermioniche.
``Settori'' di Ramond e di Nevau-Schwarz. Caratteristiche
generali di un modello di stringa super-simmetrica.
- 07-10-09:
I 5 modelli consistenti di super-stringa:
- Tipo
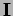
- Tipo
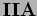
- Tipo

- Eterotica
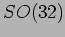
- Eterotica
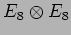
- 09-10-09:
vuoti di Calabi-Yau ed aspetti fenomenologici
della stringa Eterotica
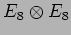 .
.
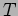 -dualità ed
-dualità ed 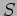 -dualità. Super-stringhe in regime
non-perturbativo.
``Fatti e congetture'' sulla
-dualità. Super-stringhe in regime
non-perturbativo.
``Fatti e congetture'' sulla
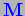 -Theory.
-Theory.
L' ``alba'' della Teoria delle Stringhe
- 09-10-09: aspetti fenomenologici delle Interazioni Forti,
negli anni `60. Risonanze Adroniche e traiettorie di Regge.
La ``Matrice-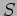 ''.
''.
- 13-10-09:
Simmetrie della Matrice-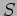 : invarianza di Poincarè;
Unitarietaà; Analiticità.
: invarianza di Poincarè;
Unitarietaà; Analiticità.
- 13-10-09:
Analiticità e Macro-Causalità. Simmetria di Crossing. Ipotesi di
``Bootstrap''.
- 14-10-09:
Limite di Regge dell'ampiezza di scattering in onde parziali.
ES.Ricavare la traiettoria di Regge (classica) per una sbarra
rigida, omogenea, rotante attorno al suo centro di massa. Si assuma che
le estremita` della sbarra si muovano alla velocità della luce.
- 14-10-09:
ES. Determinare le traiettorie di Regge per un oscillatore armonico
quantistico, non-relativistico, in 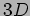 . Identificare la
``tensione'' e l' ``intercetta''. Discutere la natura quantistica di
. Identificare la
``tensione'' e l' ``intercetta''. Discutere la natura quantistica di
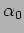 .
.
ES. Sulla base degli esercizi precedenti, ``indovinare''
la possibile forma dello spettro di una stringa, modelizzandola
come una famiglia discreta di oscillatori armonici relativistici.
Definire l' energia di punto-zero regolarizzata.
- 15-10-09:
ES.
Analizzare il contenuto del ground-state e del primo livello
eccitato.
Ripetere l' esercizio nel caso di una stringa bosonica chiusa.
- 15-10-09:
ES. Ampiezze di scattering
pione-pione in QFT: modello-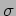 lineare.
Approssimazione di Born: andamento a
lineare.
Approssimazione di Born: andamento a 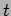 fisso
e ``grande''
fisso
e ``grande'' 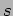 ; dipendenza dallo spin
del campo
; dipendenza dallo spin
del campo 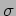 . Ampiezza ad
. Ampiezza ad 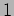 -loop e divergenze
-loop e divergenze 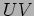 .
Modelli rinormalizzabili e non-rinormalizzabili.
.
Modelli rinormalizzabili e non-rinormalizzabili.
- 20-10-09:
Dualità tra reazioni nel canale-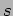 e nel canale
e nel canale 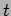 .
Ampiezza di Veneziano
per lo scattering
.
Ampiezza di Veneziano
per lo scattering
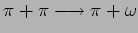 . ``Traiettorie di Regge''.
Proprietà di analiticità: rappresentazione in serie di poli.
Spettro di massa di un traiettorie di Regge.
. ``Traiettorie di Regge''.
Proprietà di analiticità: rappresentazione in serie di poli.
Spettro di massa di un traiettorie di Regge.
- 20-10-09:
ES. Ampiezza di Veneziano:
- Limite
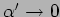
- Limite di Regge, i.e.
a momento trasferito fisso ed alta energia;
- Limite di
hard-scattering, e la fine dei Modelli Duali.
Teorie di Kaluza-Klein: alla scoperta delle
``dimensioni nascoste'' dello spazio
- 21-10-09:
La metrica in 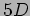 : l' ipotesi ``cilindrica'' di Kaluza:
: l' ipotesi ``cilindrica'' di Kaluza:
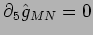 .
Trasformazioni di coordinate ``adattate'',
.
Trasformazioni di coordinate ``adattate'',
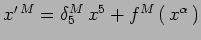 .
.
- 21-10-09:
ES Dimostrare che:
i) 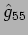 si trasforma come un scalare;
si trasforma come un scalare;
ii)
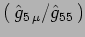 si trasfoma
come un campo di gauge abeliano con
si trasfoma
come un campo di gauge abeliano con
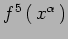 funzione di gauge.
funzione di gauge.
iii)
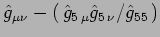 si trasforma come un tensore tipo
si trasforma come un tensore tipo 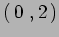 .
.
decomposizione della metrica in 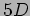 in termini di campi in
in termini di campi in 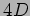 .
.
iv) Esprimere la metrica controvariante 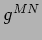 in termini
di
in termini
di 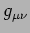 ,
,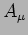 e
e 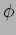 .
.
v)Calcolare
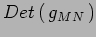 .
.
- 22-10-09:
``Riduzione Dimensionale'' dell' Azione di Einstein-Hilbert
in 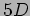 . Ipotesi di Klein: la quinta dimensione ``compatta''.
La relazione tra
. Ipotesi di Klein: la quinta dimensione ``compatta''.
La relazione tra 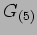 e
e 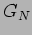 .
.
ES Studiare i ``settori di vuoto'' della teoria
ridotta dimensionalmente: nel settore di Einstein-Maxwell,
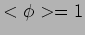 , stimare il valore di
, stimare il valore di 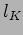
- 22-10-09:
ES Settore Dilatonico-Elettromagnetico:
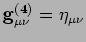 . Il
Dilatone come Bosone di Goldstone delle
Dilatazioni.
. Il
Dilatone come Bosone di Goldstone delle
Dilatazioni.
Soluzioni statiche, a simmetria sferica,
dell' equazioni di campo classiche per 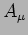 e
e
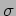 con diverse condizioni ai bordi:
con diverse condizioni ai bordi:
la Fase di Coulomb, e la Fase di
Confinamento.
Potenziale lineare e Confinamento ddlle cariche.
- 27-10-09:
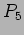 come costante del moto. Unificazione di Energia, Momento
e Carica Elettrica. Conservazione della carica ed
accoppiamento minimale.
come costante del moto. Unificazione di Energia, Momento
e Carica Elettrica. Conservazione della carica ed
accoppiamento minimale.
- 27-10-09:
ES Riduzione dimensionale dell' equazione di campo
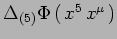 in
in
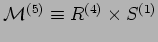 . Condizione
di periodicità in
. Condizione
di periodicità in 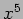 e sviluppo in serie di Fourier.
Modo-zero e modi-KK.
e sviluppo in serie di Fourier.
Modo-zero e modi-KK.
Stimare la lunghezza del cerchio 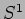 e le masse degli stati (eccitati) di Kaluza-Klein.
e le masse degli stati (eccitati) di Kaluza-Klein.
- 28-10-09:
ES Stimare in numero minimo di dimensioni dello spazio,
necessarie per descrivere, alla Kaluza-Klein, il modello
standard
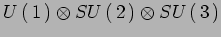 .
.
L'elettrodinamica degli oggetti estesi.
ES
Risolvere le equazioni di campo per una 3-forma,
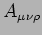 ,
in
,
in 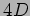 , in presenza di gravità.
, in presenza di gravità.
- 28-10-09:
ES
I Compattificazione Spontanea
nel modello di Freund-Rubin. Mostrare che le
equazioni di campo accoppiate ammettono una soluzione
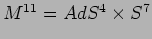 .
.
- 29-10-09:
Compattificazione Spontanea in un modello IIB di super-stringa.
Dualità
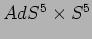 . ``Large Extra-Dimensions'' e
. ``Large Extra-Dimensions'' e
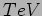 Quantum Gravity.
Quantum Gravity.
Dinamica classica e quantistica della stringa bosonica
- 29-10-09::
Variazione, ad estremi fissi, dell' azione di Nambu-Goto.
Equazioni di Eulero-Lagrange e condizioni ai bordi:
condizioni di periodicità, (stringa chiusa);
condizioni di Neumann, (stringa aperta).
Correnti di momento sulla superficie d' universo.
Conservazione del momento totale.
Vincoli e condizioni di mass-shell.
Moto delle estremità libere della stringa.
- 04-11-09:
ES Data la superficie d'universo
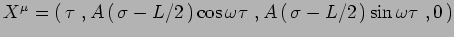
- determinare se si tratta di una stringa aperta, o chiusa.
- dimostrare che è soluzione delle equazioni classiche del moto.
- determinare il significato fisico delle costanti di integrazione
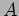 ed
ed 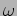 .
.
- verificare che le condizioni di mass-shell sono soddisfatte
- verificare che gli estremi della stringa si muovono alla velocità
della luce
- determinare la posizione del centro di massa della stringa
- calcolare la 3-velocità di un generico punto lungo la stringa;
- calcolare l'energia totale ed il
momento angolare totale della stringa; verifcare che
lastringa descrive una traiettoria di Regge.
- 04-11-09:
Gauge Conforme: equazioni del moto e correnti di momento.
Sviluppo in serie di Fourier per la stringa aperta con
condizioni ai bordi di Neumann.
Significato fisico delle costanti di integrazione.
Moto del centro di massa. Momento totale della stringa e condizione
di mass-shell.
- 05-11-09:
Condizioni di vincolo sulle ampiezze di Fourier. Ampiezze di Virasoro.
Spettro di massa.
Stringa chiusa: soluzione in serie di Fourier.
Modi-left e modi-right.
- 05-11-09:
ES Coordinate di cono-luce. Una particella si muove
lungo l'asse 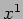 con velocita` costante
con velocita` costante 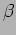 . Descrivere
il moto in coordinate di con luce nei seguenti casi:
. Descrivere
il moto in coordinate di con luce nei seguenti casi:
- 10-11-09:
ES Particella relativistica:
- scrivere l'azione canonica in coordinate di cono-luce.
- scegliere una ``gauge'' per
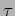
- risolvere il vincolo di mass-shell.
- definire l' Hamiltoniana di cono-luce ed identificare
le variabili fisiche
- 10-11-09:
Stringa aperta nella gauge di cono-luce. Soluzione
delle equazioni di vincolo, ed identificazione dei gradi di
libertà dinamici. Spettro di massa per i
modi trasversi. Hamiltoniana di cono-luce.
- 11-11-09:
``Prima quantizzazione'' : commutatori
canonici. Decomposizione della stringa in oscillatori armonici
quantistici. Algebra degli operatori 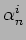 .
.
- 11-11-09:
Ambiguità di ordinamento e prescrizione di Normal
Ordering. Energia di punto-zero della stringa bosonica.
Regolarizzazione dell' energia di punto-zero mediante
cut-off esponenziale. Tre motivi per mantenere l'energia
di punto-zero:
- Effetto Casimir
- Costante Cosmologica
- Invarianza di Lorentz
Hamiltoniana di cono-luce ``regolarizzata''.
- 12-11-09:
Generatori di Lorentz quantistici.
Hermiticità ed ordinamento normale di 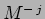 .
Operatori di Virasoro trasversi.
.
Operatori di Virasoro trasversi.
Il commutatore
![$\left[\,M^{-\,i}\ ,M^{-\,j}\,\right] $](img58.png) e
la dimensione critica dello spaziotempo.
e
la dimensione critica dello spaziotempo.
- 12-11-09:
Ordinamento normale dell' operatore numero
e l' operatore 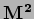 .
Gli operatori
.
Gli operatori 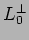 ed
ed 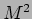 in termini dell' operatore
in termini dell' operatore
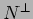 .
.
``Stati fisici della stringa.
- 17-11-09
Spettro della stringa aperta.
Calcolare gli auto-valori di
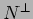 sui seguenti stati:
sui seguenti stati:
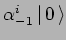 ,
,
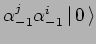
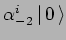 .
.
- 17-11-09:
Massa, numero di stati, spin
del:
 Ground State;
Ground State;
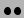 Primo livello eccitato;
Primo livello eccitato;
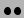 Secondo livello eccitato.
Secondo livello eccitato.
 Traiettorie di Regge quantistiche.
Traiettorie di Regge quantistiche.
- 17-11-09:
Soluzioni classiche per la stringa aperta con condizioni
ai bordi di Dirichlet lungo una direzione, e condizioni
di Neumann lungo tutte le altre.
Moto delle stremità libere. 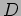 -brane.
-brane.
- 18-11-09:
Spettro di massa in funzione della distanza delle due
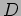 -brane parallele. Distanza critica. Il ``Meccanismo
di Higgs'' in teorie di stringa/
-brane parallele. Distanza critica. Il ``Meccanismo
di Higgs'' in teorie di stringa/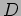 -brane.
-brane.
- 18-11-09:
I 4 ``settori'' di un modello di due 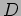 -brane parallele: forma
esplicita di
-brane parallele: forma
esplicita di 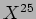 e di
e di 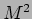 .
.
Stati di Vuoto nei vari settori.
Primo livello eccitato nei vari settori. Invarianza di gauge
e ``rottura''
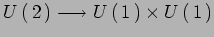 ; campi di gauge
massless e massivi.
; campi di gauge
massless e massivi.
- 19-11-09:
Indici di Chan-Paton e campi non-Abeliani.
Teorie di Yang-Mills come ``teorie efficaci''
per le eccitazioni più basse di un sistema di 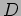 -brane.
-brane.
Invarianza di gauge e rottura di simmetria in un sistema di
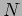
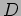 -brane parallele.
-brane parallele.
- 19-11-09:
Stringa chiusa: identificazione dei modi-zero left e right;
soluzione delle condizione di vincolo per 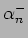 ed
ed
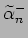 . Spettro di massa per
la stringa chiusa. Massa e spin per lo stato fondamentale
. Spettro di massa per
la stringa chiusa. Massa e spin per lo stato fondamentale
- 24-11-09:
Primo livello eccitato: il ``settore universale''.
Modello sigma non-lineare per la stringa e
teoria di campo efficace per il settore universale.
Il Dilatone e la costante di accoppiamento della stringa chiusa.
- 24-11-09:
Stringa chiusa in
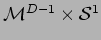 .
Modi di winding e Modi di Kaluza-Klein.
Operatori di Virasoro e condizioni di vincolo sugli stati fisici.
.
Modi di winding e Modi di Kaluza-Klein.
Operatori di Virasoro e condizioni di vincolo sugli stati fisici.
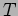 -Dualità dello stato di vuoto. Raggio di compattificazione
Autoduale.
-Dualità dello stato di vuoto. Raggio di compattificazione
Autoduale.
Stati di vuoto nei settori : 1) 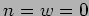 ; 2)
; 2) 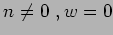 ;
; 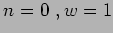 .
.



Next: About this document ...
Euro Spallucci
2009-11-20