


Next: About this document ...
Introduzione alla Teoria delle Stringhe
A.A. 2006-07
Introduzione e discussione generale
- 03-10-06:
Motivazioni ed obiettivi del corso. Testi di
riferimento. Cosa NON è la
Teoria delle Stringhe: preconcetti ed idee sbagliate.
- 03-10-06:
Motivazioni a favore della Teoria delle Stringhe.
Cosa, fondamentalmente, è una ``stringa''. I cinque
modelli di super-stringhe, e la 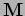 -Theory
-Theory
- 04-10-06:
Dalla Fisica del ``punto materiale'' a quella della ``linea''.
Tensione della stringa. Dinamica del punto vs Dinamica
della stringa.
- 04-10-06:
``Particelle elementari'' come modi vibrazionali della
stringa. Particelle ``leggere'' e stringhe eccitate al primo
livello. Bosoni/Fermioni come differenti modi vibrazionali
della stringa.
- 05-10-06:
``Manifold della stringa'' ; Coordinate
della stringa; ``Spazio(tempo) Targhetta'';
Superficie d' universo.; bi-vettore tangente;
Metrica Indotta; l' Azione di Nambu-Goto ed il
suo significato geometrico.
- 05-10-06:
Limite non-relativistico dell' azione di Nambu-Goto. Es. la stringa
rigida. Metrica indotta, e metrica della stringa.
Azione di Nambu-Goto in termini della metrica indotta. Invarianza
per ri-parametrizzazioni.
- 0-10-06:
L' azione di Polyakov. Proprietà di simmetria:
- Invarianza di Lorentz come ``simmetria interna'';
- Invarianza per ri-parametrizzazioni;
- Invarianza di Weyl
Equazioni di campo.
- 0-10-06:
Equivalenza classica tra l'azione di Polyakov e l'azione di
Nambu-Goto. Gauge conforme. Equazioni di vincolo, e variabili
dinamiche indipendenti.
- 11-10-06:
Incompatibilità tra Invarianza di Lorentz e quantizzazione:
il concetto di ``dimensione critica'' dello spaziotempo.
- 11-10-06:
Interazione tra stringhe e ``smearing'' del
vertice d' interazione. L' idea di ``Lunghezza minima''
in teorie di stringa.
L' ``alba'' della Teoria delle Stringhe
- 12-10-06:
Risonanze Adroniche e Chew-Frautchi plot. Ampiezze di scattering
pione-pione in Approssimazione di Born: andamento a 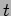 fisso
e ``grande''
fisso
e ``grande'' 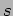 .
.
- 12-10-06:
Ampiezze di scattering
pione-pione in Approssimazione di Born: dipendenza dallo spin
dell' oggetto scambiato. Modelli rinormalizzabili e
non-rinormalizzabili. Poli nel canale-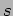 e poli nel canale
e poli nel canale 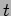 .
Dualità.
.
Dualità.
- 16-10-06:
Ampiezza di Veneziano per lo scattering
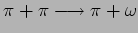 . ``Traiettorie di Regge''.
Proprietà di analiticità: rappresentazione in serie di poli.
. ``Traiettorie di Regge''.
Proprietà di analiticità: rappresentazione in serie di poli.
- 16-10-06:
Spettro di massa di un traiettorie di Regge e spin come funzione
del momento trasferito, i.e.
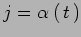 .
Andamento dell'ampiezza di Veneziano nel limite di Regge, i.e.
a momento trasferito fisso ed alta energia.
.
Andamento dell'ampiezza di Veneziano nel limite di Regge, i.e.
a momento trasferito fisso ed alta energia.
- 17-10-06:
Ricavare la traiettoria di Regge (classica) per una sbarra rigida,
omogenea, rotante attorno al suo centro di massa. Si assuma che
le estremita` della sbarra si muovano alla velocità della luce.
Determinare le traiettorie di Regge per un oscillatore armonico
quantistico, non-relativistico, in 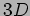 . identificare la
``tensione'' e l' ``intercetta''. Discutere la natura quantistica di
. identificare la
``tensione'' e l' ``intercetta''. Discutere la natura quantistica di
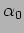 .
.
- 17-10-06:
Sulla base degli esercizi precedenti, fare un ``guess'' sulla
possibile forma dello spettro di una stringa, modelizzandola
come una famiglia di oscillatori armonici relativistici.
Definire l' energia di punto-zero regolarizzata.
Lo stato fondamentale della stringa bosonica: il problema del
``tachione''.
L' andamento dell' ampiezza di Veneziano nel limite di
hard-scattering, e la fine dei Modelli Duali.
Teorie di Kaluza-Klein: alla scoperta delle
``dimensioni nascoste'' dello spazio
- 19-10-06:
La metrica in 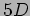 : l' ipotesi ``cilindrica'' di Kaluza.
: l' ipotesi ``cilindrica'' di Kaluza.
Dimostare che, se
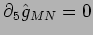 vale in ogni sistema di coordinate, allora, segue che
vale in ogni sistema di coordinate, allora, segue che
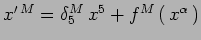 .
.
Dimostrare che:
i) 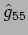 si trasforma come un scalare;
si trasforma come un scalare;
ii)
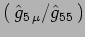 si trasfoma
come un campo di gauge abeliano con
si trasfoma
come un campo di gauge abeliano con
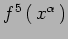 funzione di gauge.
funzione di gauge.
- 19-10-06:
Dimostrare che:
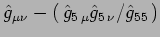 si trasforma come un tensore tipo
si trasforma come un tensore tipo 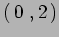 .
.
decomposizione della metrica in 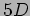 in termini di campi in
in termini di campi in 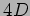 .
.
- 24-10-06:
Esprimere la metrica controvariante 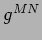 in termini di
in termini di 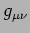 ,
,
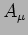 e
e 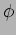 . Calcolare
. Calcolare
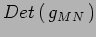 .
Assumendo che la gravità in
.
Assumendo che la gravità in 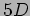 sia descritta da
sia descritta da
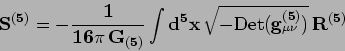 |
(1) |
ricavare la relazione tra 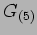 e
e 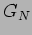 .
.
Riscalo conforme,
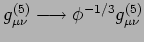 ed
azione nell' ``Einstein Frame''.
ed
azione nell' ``Einstein Frame''.
- 24-10-06:
Settore di Einstein-Maxwell:
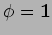 .
Ricavare
.
Ricavare
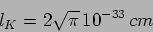 |
(2) |
Settore di Brans-Dicke:
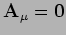 .
Teorie scalari-tensori della gravità.
.
Teorie scalari-tensori della gravità.
Settore Dilatonico-Elettromagnetico:
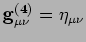 . Il
Dilatone.
. Il
Dilatone.
- 25-10-06:
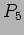 come costante del moto. Unificazione di Energia, Momento
e Carica Elettrica.
come costante del moto. Unificazione di Energia, Momento
e Carica Elettrica.
Riduzione dimensionale dell'equazione delle geodetiche da 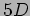 a
a 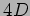 .
.
- 25-10-06:
O. Klein e la compattificazione della quinta dimensione:
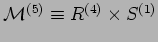 . Condizione
di periodicità in
. Condizione
di periodicità in 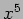 e sviluppo in serie di Fourier.
Modo-zero e modi-KK.
Riduzione dimensionale dell' equazione di campo
e sviluppo in serie di Fourier.
Modo-zero e modi-KK.
Riduzione dimensionale dell' equazione di campo
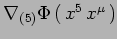 .
.
- 26-10-06:
Studiare lo spettro di un campo
di Klein-Gordon, a massa nulla, in
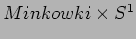 .
Stimare la lunghezza del cerchio
.
Stimare la lunghezza del cerchio 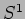 utilizando la relazione tra la carica elettrica ed
utilizando la relazione tra la carica elettrica ed 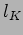 .
.
- 26-10-06:
Il problema della Compattificazione Spontanea.
Il modello di Freund-Rubin.
`` Large extra-dimensions'' ed Unificazione al 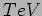 .
.
Dinamica classica e quantistica della stringa bosonica
- 31-10-06:
Variazione, ad estremi fissi, dell' azione di Nambu-Goto.
Equazioni di Eulero-Lagrange e condizioni ai bordi:
condizioni di periodicità, (stringa chiusa);
condizioni di Neumann, (stringa aperta);
condizioni di Dirichlet, (stringa aperta).
- 31-10-06:
Correnti di momento sulla superficie d' universo.
Vincoli e condizioni di mass-shell.
Moto delle estremità libere della stringa.
Soluzione delle equazioni del moto per una stringa rigida,
aperta: lunghezza propria e lunghezza di coordinate.
- 2-11-06:
Soluzione delle equazioni del moto per una stringa rigida,
aperta: condizioni ai bordi di Neumann; moto delle estremita`
libere; velocità di un generico punto lungo la stringa;
posizione del centro di massa nello spaziotempo traghetta;
mass/energy e momento angolare totale, traiettoria di Regge.
- 2-11-06:
Gauge Conforme: equazioni del moto e correnti di momento.
Sviluppo in serie di Fourier per la stringa aperta con
condizioni ai bordi di Neumann. Moto del centro di massa.
Momento totale e condizione di mass-shell.
- 7-11-06:
Stringa aperta: soluzione in serie di Fourier; costanti di integrazione.
Moto del centro di massa. Momento totale della stringa e condizione
di mass-shell.
- 7-11-06:
Condizioni di vincolo sulle ampiezze di Fourier. Ampiezze di Virasoro.
Spettro di massa.
Stringa chiusa: soluzione in serie di Fourier.
- 8-11-06:
Stringa chiusa: modi-left e modi-right. Spettro di massa.
Coordinate di cono-luce, aspetti cinematici e dinamica della
particella relativistica.
- 8-11-06:
Stringa aperta nella gauge di cono-luce. Equazioni
di vincolo per le ampiezze di Fourier. Spettro di massa per i
modi trasversi.
- 9-11-06:
Hamiltoniana di cono-luce. ``Prima quantizzazione'' : commutatori
canonici. Decomposizione della stringa in oscillatori armonici
quantistici. Algebra degli operatori 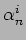 .
.
- 9-11-06:
Ambiguità di ordinamento e prescrizione di Normal
Ordering. Energia di punto-zero della stringa bosonica.
Regolarizzazione dell' energia di punto-zero mediante:
a) funzione Zeta di Riemann;
b) cut-off esponenziale.
Energia di punto-zero di oscillatori fermionici.
- 14-11-06:
Stringa come famiglia infinita di oscillatori armonici quantistici:
forma canonica del commutatore.
Generatori di Lorentz in termini dei modi di oscillazione.
Hermiticità ed ordinamento normale di 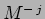 .
Operatori di Virasoro trasversi.
.
Operatori di Virasoro trasversi.
- 14-11-06:
Il commutatore
![$\left[ M^{- i} ,M^{- j} \right] $](img40.png) e
la dimensione critica dello spaziotempo.
e
la dimensione critica dello spaziotempo.
Ordinamento normale dell' operatore numero
e l' operatore 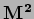 .
.
- 15-11-06:
Gli operatori 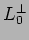 ed
ed 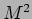 in termini dell' operatore
in termini dell' operatore
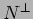 .
.
Lo ``stato di vuoto della stringa.
Base nello spazio di Hilbert tramite auto-stati di 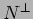 .
.
Es. Calcolare gli auto-valori di 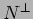 sui seguenti stati:
sui seguenti stati:
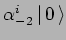 ,
,
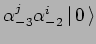 .
.
- 15-11-06:
Spettro della stringa aperta. Massa e numero di stati presenti nel:
 Ground State;
Ground State;
 Primo livello eccitato;
Primo livello eccitato;
 Secondo livello eccitato;
Secondo livello eccitato;
Il ``Tachione'' e l' instabiltà del vuoto.
- 16-11-06:
Soluzioni classiche per la stringa aperta con condizioni
ai bordi di Dirichlet lungo una direzione, e condizioni
di Neumann lungo tutte le altre. Moto delle stremità
libere. 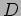 -brane.
-brane.
- 16-11-06:
Spettro di massa in funzione della distanza delle due
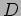 -brane parallele. Distanza critica. Il ``Meccanismo
di Higgs'' .
-brane parallele. Distanza critica. Il ``Meccanismo
di Higgs'' .
- 21-11-06:
I 4 ``settori'' di un modello di due 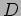 -brane parallele: forma
esplicita di
-brane parallele: forma
esplicita di 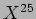 e di
e di 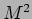 .
.
Stati di Vuoto nei vari settori.
Primo livello eccitato nei vari settori. Invarianza di gauge
e ``rottura''
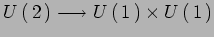 ; campi di gauge
massless e massivi.
; campi di gauge
massless e massivi.
- 21-11-06:
Indici di Chan-Paton e campi non-Abeliani.
Teorie di Yang-Mills come ``teorie efficaci''
per le eccitazioni più basse di un sistema di 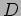 -brane.
-brane.
Invarianza di gauge e rottura di simmetria in un sistema di
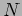
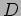 -brane parallele
-brane parallele
- 22-11-06:
Modelli a 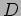 -brane ed il problema del confinamento in
-brane ed il problema del confinamento in 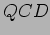 .
.
Congetture sulla 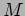 -theory.
-theory.
- 22-11-06:
Stringa chiusa: identificazione dei modi-zero left e right;
soluzione delle condizione di vincolo per 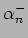 ed
ed
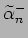 .
.
- 23-11-06:
Operatori di Virasoro, Hamiltoninano e spettro di massa per
la stringa chiusa. Massa e spin per lo stato fondamentale
ed il primo livello eccitato.
- 23-11-06:
Teoria di campo efficace per la stringa chiusa, in termini
del Dilatone, Gravitone e potenziale di Kalb-Ramond.
Il Dilatone e la costante di accoppiamento della stringa chiusa.
L' azione di Einstein come approssimazione di ordine-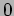 in
in
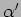 dell'azione per il gravitone.
dell'azione per il gravitone.
- 28-11-06:
Il campo di Kalb-Ramond come ``mediatore'' dell' interazione
``elettro-magnetica'' tra stringhe chiuse.
Stringa chiusa in
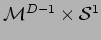 .
Modi di winding e Modi di Kaluza-Klein.
.
Modi di winding e Modi di Kaluza-Klein.
- 28-11-06:
Spettro della stringa chiusa in
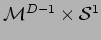 .
Stati di vuoto nei settori : 1)
.
Stati di vuoto nei settori : 1) 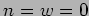 ; 2)
; 2) 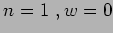 ;
; 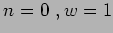 .
.
Stati con 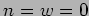 : Settore di vuoto,
: Settore di vuoto,
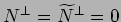 ;
Settore massless,
;
Settore massless,
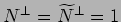 , intepretazione
dei campi via riduzione dimensionale alla Kaluza-Klein ed invarianza
di gauge
, intepretazione
dei campi via riduzione dimensionale alla Kaluza-Klein ed invarianza
di gauge
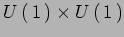 .
.
Homeworks
- Dimostrare che il D'Alembertiano covariante sugli scalari
si scrive come:
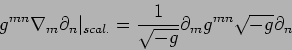 |
(3) |
Ricavare la forma esplicita del tensore energia impulso della
stringa dalla definizione
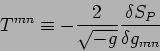 |
(4) |
- Si consideri una ri-parametrizzazione infinitesima
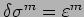 . Dimostrare che dall' invarianza
dell' azione deriva:
. Dimostrare che dall' invarianza
dell' azione deriva:
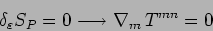 |
(5) |
Cosa implica la condizione
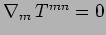 ?
?
Si consideri una trasformazione di Weyl infinitesima
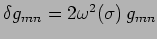 .
Dimostrare che dall' invarianza
dell' azione deriva:
.
Dimostrare che dall' invarianza
dell' azione deriva:
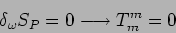 |
(6) |
- Variabili di Mandelstam. Dimostrare che
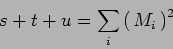 |
(7) |
- Dimostrare che:
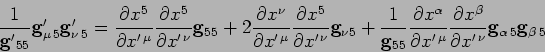 |
(8) |
- Ricavare le equazioni di campo per
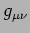 ,
, 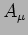 ,
, 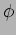 dall' azione:
dall' azione:
![\begin{displaymath}
\mathbf{ S^{(5)}= - \frac{1}{16\pi G_N}\int d^4x
\sqrt...
...}g^{(4) \mu\nu}\partial_\mu\phi \partial_\nu\phi \right]
}
\end{displaymath}](img75.png) |
(9) |
- Dimostrare che
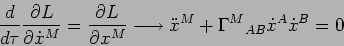 |
(10) |
- verificare che
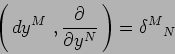 |
(11) |
con
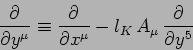 |
(12) |
- Calcolare
![\begin{displaymath}
\left[ \frac{\partial }{\partial {y}^\mu} ,
\frac{\partial }{\partial {y}^\nu} \right]=?
\end{displaymath}](img79.png) |
(13) |



Next: About this document ...
Euro Spallucci
2008-08-08
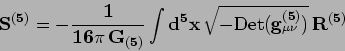
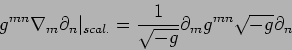
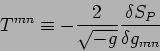
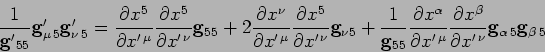
![\begin{displaymath}
\mathbf{ S^{(5)}= - \frac{1}{16\pi G_N}\int d^4x
\sqrt...
...}g^{(4) \mu\nu}\partial_\mu\phi \partial_\nu\phi \right]
}
\end{displaymath}](img75.png)
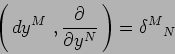
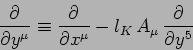
![\begin{displaymath}
\left[ \frac{\partial }{\partial {y}^\mu} ,
\frac{\partial }{\partial {y}^\nu} \right]=?
\end{displaymath}](img79.png)