Next: About this document ...
Introduzione alla Teoria delle Stringhe
A.A. 2002-03
Modelli Duali:
le Interazioni Forti nei
``favolosi anni `60''.
- 01-10-02:
Motivazioni e struttura del corso. Testi di
riferimento e materiale didattico on-line. Aspetti fenomenologici
della fisica delle Interazioni Forti negli anni '60. Variabili
di Mandelstam ed invarianza delle ampiezze elastiche per scambio
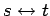 .
.
- 01-10-02:
Eserc.1
Si consideri l'urto
elastico
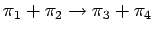 . Determinare
la dipendenza da
. Determinare
la dipendenza da 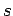 e
e 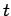 dell' ampiezza elastica di Born, nell' ipotesi
che:
dell' ampiezza elastica di Born, nell' ipotesi
che:
i) nel canale-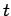 sia scambiata una particella di spin-
sia scambiata una particella di spin-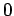 ;
;
ii) nel canale-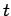 sia scambiata una particella di spin-
sia scambiata una particella di spin-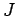 ;
;
iii) si determinini l'andamento dell' ampiezza ad ``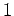 -loop''
in funzione delllo spin-
-loop''
in funzione delllo spin-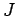 della particella scambiata.
della particella scambiata.
- 02-10-02:
Ampiezze elastiche come ``somme infinite di poli''
nel canale-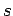 e nel canale-
e nel canale-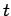 . La `` Dualità'' e
l' Ampiezza di Veneziano. Le Traiettorie di Regge.
. La `` Dualità'' e
l' Ampiezza di Veneziano. Le Traiettorie di Regge.
- 02-10-02:
Eserc.2
Utilizzando le
proprietà
di analiticità della Funzione-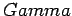 di Eulero, dimostrare che
l' ampiezza di Veneziano ha solo poli semplici nel canale-
di Eulero, dimostrare che
l' ampiezza di Veneziano ha solo poli semplici nel canale-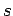 e nel
canale-
e nel
canale-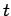 .
.
Ricavare la massa dell' oggetto scambiato nel canale-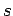 o nel
canale-
o nel
canale-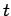 in funzione dei parametri
in funzione dei parametri 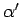 ed
ed 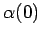 della traiettoria di Regge; verificare la relazione lineare
tra spin e massa al quadrato dell' oggetto medesimo.
della traiettoria di Regge; verificare la relazione lineare
tra spin e massa al quadrato dell' oggetto medesimo.
Utilizzando la formula di Stirling determinare l'andamento
asintotico dell' ampiezza di Veneziano a ``grandi 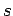 e
e 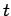 fissato''.
fissato''.
- 14-10-02:
Eserc.3
Calcolare la massa
totale 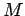 ed il momento angolare
ed il momento angolare 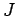 di una sbarra rigida, ruotante
attorno al suo centro di massa in mod tale che le estremità abbiano
velocità pari a quella della luce; determinare la relazione tra
di una sbarra rigida, ruotante
attorno al suo centro di massa in mod tale che le estremità abbiano
velocità pari a quella della luce; determinare la relazione tra
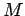 e
e 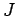 .
.
Andamento dell' ampiezza di Veneziano ad alta energia ed angolo
di diffusione fisso. La fine dei modelli adronici a stringa.
Teorie di Kaluze-Klein: viaggio guidato nella
``quinta dimensione'' ...ed oltre!
- 14-10-02:
La gravità in cinque dimensioni. La `` quinta dimensione'' e
l' ipotesi di Kaluza:
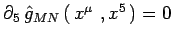 .
.
- 15-10-02:
Eserc.4 Dimostare che, se
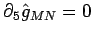 vale in ogni sistema di coordinate, allora, segue che
vale in ogni sistema di coordinate, allora, segue che
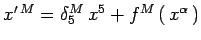 .
.
Dimostrare che:
i) 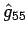 si trasforma come un scalare;
si trasforma come un scalare;
ii)
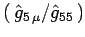 si trasfoma
come un
campo di gauge abeliano con
si trasfoma
come un
campo di gauge abeliano con
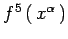 funzione di gauge;
funzione di gauge;
iii)
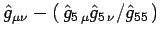 si trasforma come un tensore tipo
si trasforma come un tensore tipo 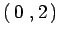 ;
;
- 15-10-02:
Forma generale della metrica di Kaluza-Klein in termini di
campi 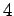 -dimensionali. Coefficienti di Connessione ed equazione
delle geodetiche in
-dimensionali. Coefficienti di Connessione ed equazione
delle geodetiche in 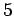 -dimensioni.
-dimensioni.
- 16-10-02:
Eserc.5
Dimostrare che
la componente-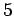 del momento lineare è una costante del moto
in
del momento lineare è una costante del moto
in 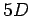 .
.
Dimostrare che
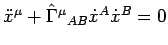 è equivalente a
è equivalente a
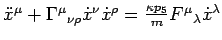 .
.
Dimostrare che
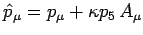 .
.
- 16-10-02:
L' ``unificazione'' di energia-momento-carica.
La quinta dimensione come `` cerchio'' 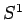 . Modo-zero e
livelli eccitati di un campo in
. Modo-zero e
livelli eccitati di un campo in 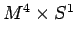 .
Il signifcato di
.
Il signifcato di
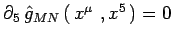 .
.
Eserc.6
Studiare lo spettro di un campo
di Klein-Gordon, a massa nulla, in
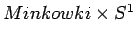 .
.
- 21-10-02 :
Eserc.7
Stimare la lunghezza del cerchio 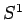 utilizando la relazione tra la carica elettrica e
utilizando la relazione tra la carica elettrica e 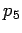 .
.
Dall' azione
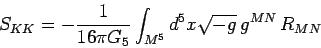 |
(1) |
ricavare l'azione efficace per il ``modo-zero'' della metrica
di Kaluza-Klein. ( Riduzione dimensionale )
- 21-10-02 :
Eserc. 8
Ricavare la relazione tra 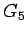 ,
, 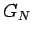 ,
ed
,
ed 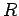 ;
;
si assuma
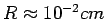 . Quanto vale
. Quanto vale 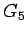 in unità naturali
?
in unità naturali
?
Si ripeta il conto precedente nel caso in cui le extra dimensioni siano
una 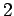 -sfera di raggio
-sfera di raggio 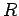 .
.
`` Large extra-dimensions'' ed Unificazione al 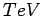 ( CENNI ).
( CENNI ).
- 22-10-02 :
La formulazione alla Kaluza-Klein delle teorie di Yang-Mills ( CENNI).
Eserc.9
Determinare il
numero minimo di dimensioni dello
spazio compatto 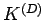 affinchè il gruppo di simmetria ``interna''
contenga
affinchè il gruppo di simmetria ``interna''
contenga
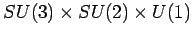 .
.
Super Gravità in 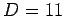 ed
ed 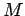 -Theory ( CENNI).
-Theory ( CENNI).
- 22-10-02 :
Eserc.10
Dimostrare che le equazioni di Einstein
in 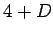 dimensioni, con
dimensioni, con 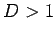 , nel vuoto non ammettono soluzioni del
tipo Minkoswki
, nel vuoto non ammettono soluzioni del
tipo Minkoswki 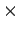 spazio compatto.
spazio compatto.
Il problema della Compattificazione Spontanea.
La soluzione di Wetterich vs il modello di Freund-Rubin.
``String-Wars I:
.... Il cono-luce sia con te!''
- 23-10-02 :
Mini-Glossario dei modelli a stringa:
``manifold d' universo''; Coordinate
della stringa; ``spazio targhetta''; Superficie
d' universo.
- 23-10-02 :
La dinamica della stringa relativistica come dinamica della
superficie d'universo. L' azione di Nambu-Goto ed il
suo significato geometrico.
La tensione della stringa.
- 24-10-02 :
Eserc.11
Scrivere l' azione di Nambu-Goto in
termini della ``metrica indotta'' sulla superficie d'universo;
dimostrare che l' azione di Nambu-Goto e` invariante per
Diffeomorfismi
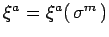 del manifold d' universo.
del manifold d' universo.
Calcolare il limite non-relativistico dell' azione di Nambu-Goto.
- 24-10-02 :
Variazione ad estremi fissi dell' azione di Nambu-Goto. Condizioni ai
bordi : periodiche ( stringa chiusa ); Neumann ( stringa aperta ).
Conservazione del flusso di momento
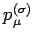 nei due casi.
Condizioni ai bordi di Dirichlet (CENNI).
nei due casi.
Condizioni ai bordi di Dirichlet (CENNI).
- 28-10-02 :
Momento lineare totale e momento angolare totale di una stringa.
Equazioni di Eulero-Lagrange per la superficie d' universo.
Vincoli e condizioni di ``mass-shell''.
- 28-10-02 :
Eserc.12
Data:
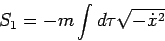 |
(2) |
dimostrare che l' Hamiltoniana canonica è identicamente nulla.
Si consideri
![\begin{displaymath}
S_2=-\int d\tau\left[\, \frac{{\dot x}^2}{2e(\tau)}-\frac{m^2}{2}
e(\tau) \,\right]
\end{displaymath}](img46.gif) |
(3) |
Come deve trasformarsi la variabile ausiliaria 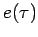 affinchè
affinchè
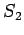 sia invariante per riparametrizzazioni?
sia invariante per riparametrizzazioni?
Dimostrare che 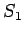 ed
ed 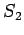 danno la stessa dinamica classica.
danno la stessa dinamica classica.
- 29-10-02 :
L' azione di Polyakov: proprietà
di simmetria e significato fisico. Equivalenza classica con
l'azione di Nambu-Goto.
- 29-10-02 :
L' azione di Polyakov nella
Gauge Conforme.
Equazioni del moto e condizioni di vincolo.
- 30-10-02 :
Eserc. 13
Calcolare 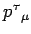 e
e
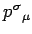 nella ``gauge conforme'', e verifcare le condizioni di vincolo.
nella ``gauge conforme'', e verifcare le condizioni di vincolo.
Risolvere le equazioni del moto
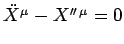 per una stringa aperta con condizioni ai bordi di Neumann tramite
serie di Fourier.
Determinare il significato fisico delle due costanti di integrazione.
per una stringa aperta con condizioni ai bordi di Neumann tramite
serie di Fourier.
Determinare il significato fisico delle due costanti di integrazione.
- 30-10-02 :
Eserc. 14
Determinare a quali condizioni devono
soddisfare le ampiezze di Fourier 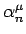 affinchè
affinchè 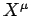 siano reali.
siano reali.
Risolvere le equazioni del moto
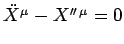 per una stringa chiusa con condizioni di
periodicitaà ai bordi tramite serie di Fourier.
per una stringa chiusa con condizioni di
periodicitaà ai bordi tramite serie di Fourier.
- 04-11-02 :
Equazioni di vincolo in termini delle componenti di Fourier
del tensore energia impulso. 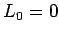 come spettro di massa
della stringa classica.
come spettro di massa
della stringa classica.
- 04-11-02 :
Invarianza di gauge `` residua'' nella gauge conforme.
Coordinate di cono-luce nello spazio targhetta.
- 05-11-02 :
Risoluzione delle equazioni dei vincoli in coordinate di cono-luce.
Gradi di libertà fisici.
- 05-11-02 :
Eserc.15
Calcolare lo spettro di massa 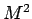 nella gauge di cono-luce in funzione delle ampiezze di Fourier.
nella gauge di cono-luce in funzione delle ampiezze di Fourier.
Determinare l' Hamiltoniana nella gauge di cono-luce.
``String-Wars II:
... Il cono-luce colpisce ancora!''
- 06-11-02 :
Commutatori Canonici. Algebra degli operatori 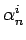 ,
,
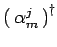 , i.e. l' algebra degli
oscillatori armonici quantistici della stringa.
, i.e. l' algebra degli
oscillatori armonici quantistici della stringa.
- 06-11-02 :
Ambiguità di ordering. Normal ordering. L' operatore
Hamiltoniano di cono-luce. Energia di punto-zero
della stringa.
- 11-11-02 :
Eserc. 16
Calcolare l`` Energia di Casimir'' della
stringa, definita come:
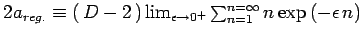 ; determinare
; determinare 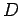 in modo che
in modo che 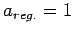 affinche` l'
invarianza di Lorentz sia preservata.
affinche` l'
invarianza di Lorentz sia preservata.
Ripetere il conto aggiungendo il contributo di ``oscillatori fermionici''
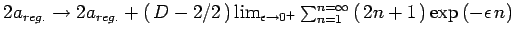 ; calcolare il corrispondente
valore di
; calcolare il corrispondente
valore di 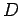 .
.
- 11-11-02 :
Operatori `` Numero di Occupazione.'' e ``
Massa al Quadrato.''.
Lo Stato Fondamentale della stringa bosonica (aperta)
Il primo livello eccitato della stringa bosonica (aperta) ed il problema
dell' invarianza di Lorentz.
- 12-11-02 :
Eserc. 17
Calcolare gli autovalori dell'operatore 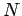 , numero di
occupazione sui seguenti stati:
, numero di
occupazione sui seguenti stati:
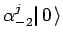 ;
;
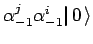 . Dimostrare che
il numero di stati presenti sul livello
. Dimostrare che
il numero di stati presenti sul livello 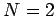 è lo stesso delle
componenti di un tensore simmetrico, a traccia nulla, di rango
è lo stesso delle
componenti di un tensore simmetrico, a traccia nulla, di rango 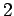 in D=26; calcolare la massa di questo oggetto.
in D=26; calcolare la massa di questo oggetto.
- 12-11-02 :
Lo spettro di massa della stringa bosonica e le
traiettorie di Regge: ancora 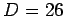 .
.
L' invarianza di Lorentz in coordinate di cono-luce: 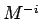 come possibili generatori anomali.
come possibili generatori anomali.
- 13-11-02 :
Eserc. 18
Calcolare il commutatore:
![$\left[\, \alpha^i_m\
,\alpha^-_n\,\right]$](img69.gif) .
.
Calcolare il commutatore:
![$\left[\,\alpha^-_m\ ,\alpha^-_n\,
\right]$](img70.gif) .
.
- 13-11-02 :
L' Algebra di Virasoro come ``estensione centrale''
dell' algebra dei diffeomorfismi sul cerchio, i.e. l'
Anomalia dell'algebra degli operatori di Virasoro 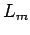 .
Le identità di Jacobi per gli
.
Le identità di Jacobi per gli 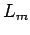 e l' equazione
per il termine anomalo in
e l' equazione
per il termine anomalo in
![$\left[\, L_m\ , L_n\,\right]$](img72.gif) .
.
- 18-11-02 :
Eserc. 19
Calcolare
![$\langle\, 0\,\vert \,\left[\, L_1\ , L_{-1}\,\right]
\,\vert \, 0\,\rangle $](img73.gif)
Calcolare
![$\langle\, 0\,\vert \,\left[\, L_2\ , L_{-2}\,\right]
\,\vert \, 0\,\rangle $](img74.gif)
Calcolare i coefficienti 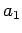 ed
ed 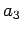 della carica centrale.
della carica centrale.
- 18-11-02 :
Quantizzazione canonica della stringa bosonica chiusa. Operatore
Hamiltoniano ed operatore 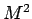 . Stato fondamentale: Tachione.
Primo livello eccitato: gravitone, dilatone,
potenziale di Kalb-Ramond.
. Stato fondamentale: Tachione.
Primo livello eccitato: gravitone, dilatone,
potenziale di Kalb-Ramond.
- 19-11-02 :
Eserc. 20
Calcolare lo spettro di massa per una stringa chiusa
in uno spazio targhetta con
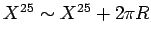 .
.
- 19-11-02 :
Winding Number e livelli di eccitazione topologici.
Quantizzazione di 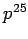 e stati eccitati di Kaluza-Klein.
T-Dualità e le sue conseguenze fisiche.
e stati eccitati di Kaluza-Klein.
T-Dualità e le sue conseguenze fisiche.
- 20-11-02 :
Eserc. 21
Calcolare lo spettro di massa per una stringa aperta con
condizioni ai bordi di Neumann su
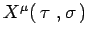 per
per
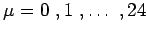 , e condizioni di Dirichlet per
, e condizioni di Dirichlet per
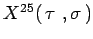 :
:
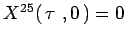 ,
,
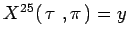 ;
;
si studi, in particolare, la massa del ``fotone'', i.e.
il primo livello eccitato della stringa aperta.
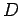 -Brane e Meccanismo di Higgs (CENNI)
-Brane e Meccanismo di Higgs (CENNI)
- 20-11-02 :
L' interazione fondamentale per stringhe aperte e stringhe
chiuse. Sviluppo perturbativo dell' ampiezza di scattering
come ``sviluppo nella topologia'' della superificie d' universo.
Scattering On-Shell.
- 25-11-02 :
Eserc. 22
Si consideri l' urto elastico (tra particelle):
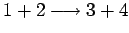 al ``tree-level'', nel canale-s.
Ricavare una rappresentazione a ``path-integral'' per l'ampiezza
di scattering.
al ``tree-level'', nel canale-s.
Ricavare una rappresentazione a ``path-integral'' per l'ampiezza
di scattering.
- 25-11-02 :
Eserc. 23
Dimostrare che il path-integral nell'ampiezza di scattering
puo` essere ricavato sia:
i) tramite una teoria di campo; sia
ii) tramite un integrale sui cammini di tipo quanto-meccanico.
Ricavare l'espressione :
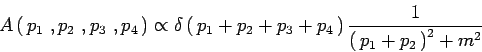 |
(4) |
- 26-11-02 :
Lo scattering elastico stringa-stringa al tree-level.
Operatori di vertice e rappresentazione a ``path integral''
per l'ampiezza di scattering.
- 26-11-02 :
Ampiezza elastica tachione-tachione:
integrazione gaussiana sulle coordinate di stringa e contributo
dei modi-zero. Regolarizzazione della funzione di Green in 2D.
- 27-11-02 :
Simmetria residua dell'ampiezza di scattering
per trasformazioni di scala globali della misura d' integrazione.
Gauge fixing. Rinormalizzazione della costante di accopiamento.
- 27-11-02
L' Ampiezza di Virasoro-Shapiro. Invarianza per scambio
delle variabili di Mandelstam. Andamento alla Regge.
Limite di ``hard-scattering''.



Next: About this document ...
Euro Spallucci
2002-12-27
![\begin{displaymath}
S_2=-\int d\tau\left[\, \frac{{\dot x}^2}{2e(\tau)}-\frac{m^2}{2}
e(\tau) \,\right]
\end{displaymath}](img46.gif)